题目内容
若f(x)=x2+(4cosθ)x-1在[1,
]上为增函数,则θ的取值范围是( )
| 3 |
A、[2kπ-
| ||||
B、[2kπ-
| ||||
C、[2kπ+
| ||||
D、[2kπ-
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:由题意可得-2cosθ≤1,求得cosθ≥-
,可得x的范围.
| 1 |
| 2 |
解答:
解:由于二次函数 f(x)=x2+(4cosθ)x-1的对称轴方程为x=-2cosθ,函数在[1,
]上为增函数,
∴-2cosθ≤1,求得cosθ≥-
,∴x∈[2kπ-
,2kπ+
](k∈Z),
故选:A.
| 3 |
∴-2cosθ≤1,求得cosθ≥-
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
故选:A.
点评:本题主要考查二次函数的性质,余弦函数的图象特征,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x0是函数f(x)=(
)x+
的一个零点,若x1∈(-∞,x0),x2∈(x0,-1),则( )
| 1 |
| 2 |
| 1 |
| 1+x |
| A、f(x1)<0,f(x2)<0 |
| B、f(x1)<0,f(x2)>0 |
| C、f(x1)>0,f(x2)<0 |
| D、f(x1)>0,f(x2)>0 |
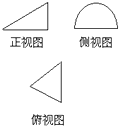 如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
执行如图所示的程序框图,输出的S值为( )

| A、144 | B、36 |
| C、49 | D、169 |
已知x、y满足条件
,则4x+2y的最小值为( )
|
| A、5 | B、-5 | C、12 | D、-12 |
已知函数y=f(x)是奇函数,当x≥0,f(x)=3x-1,设f(x)的反函数是y=g(x),则g(-8)=( )
| A、-2 | B、2 | C、-3 | D、3 |
若直线y=2ax-2与y=(a+2)x+1平行,则a=( )
| A、2 | B、1 | C、-1 | D、0 |