题目内容
若(x+
)n的二项式展开式中二项式系数之和为64，则展开式中的常数项为（ ）
| 1 |
| x |
| A、10 | B、20 | C、30 | D、35 |
考点：二项式系数的性质
专题：二项式定理
分析：由二项式系数之和为64，求得n=6，在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项．
解答：
解：由于(x+
)n的二项式展开式中二项式系数之和为2n=64，可得n=6，
故展开式的通项公式为Tr+1=
•x6-2r，令6-2r=0，求得r=3，
可得展开式中的常数项为
=20，
故选：B．
| 1 |
| x |
故展开式的通项公式为Tr+1=
| C | r 6 |
可得展开式中的常数项为
| C | 3 6 |
故选：B．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
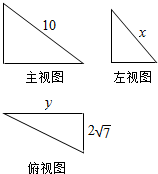
某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy的最大值为（ ）
| A、32 | ||
B、32
| ||
| C、64 | ||
D、64
|
已知定义域为R的函数f（x）不是奇函数，给定下列4个命题：
①函数g（x）=f（-x）-f（x）是奇函数；
②?x∈R，f（-x）≠-f（x）；
③?x∈R，f（-x）=f（x）；
④?x0∈R，f（-x0）≠-f（x0）．
其中为真命题的命题是（ ）
①函数g（x）=f（-x）-f（x）是奇函数；
②?x∈R，f（-x）≠-f（x）；
③?x∈R，f（-x）=f（x）；
④?x0∈R，f（-x0）≠-f（x0）．
其中为真命题的命题是（ ）
| A、①② | B、②③ | C、③④ | D、①④ |
已知向量
=（3，1），
=（-2，5），那么2
+
等于（ ）
| a |
| b |
| a |
| b |
| A、.（-1，11） |
| B、.（4，7） |
| C、.（1，6） |
| D、（5，-4） |
如图，在矩形ABCD中，E为边AD的中点，AB=1，BC=2，分别以A、D为圆心，1为半径作圆弧EB、EC（E在线段AD上）．由两圆弧EB、EC及边BC所围成的平面图形绕直线AD旋转一周，则所形成的几何体的体积为圆心在抛物线y2=2x上，且与x轴和抛物线的准线都相切的一个圆的方程是（ ）
| A、x2+y2-x-2y+1=0 | ||
B、x2+y2-x-2y-
| ||
| C、x2+y2+x-2y+1=0 | ||
D、x2+y2-x-2y+
|