题目内容
 如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A、D为圆心,1为半径作圆弧EB、EC(E在线段AD上).由两圆弧EB、EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为
如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A、D为圆心,1为半径作圆弧EB、EC(E在线段AD上).由两圆弧EB、EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为考点:组合几何体的面积、体积问题
专题:空间位置关系与距离
分析:由旋转一周得到的几何体为圆柱去掉两个半径为1的半球,利用圆柱和球的体积公式进行计算即可.
解答:
解:图中阴影部分绕AD旋转一周所形成的几何体为圆柱去掉两个半径为1的半球,
两个半球的体积为:2×
×
×π=
π.
圆柱的底面半径为1,高为2,
∴圆柱的体积为π×2=2π,
∴该几何体的体积为2π-
π=
.
故答案为:
两个半球的体积为:2×
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
圆柱的底面半径为1,高为2,
∴圆柱的体积为π×2=2π,
∴该几何体的体积为2π-
| 4 |
| 3 |
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题主要考查旋转体的体积,要求熟练掌握常见几何体的体积公式.比较基础.

练习册系列答案
相关题目
若(x+
)n的二项式展开式中二项式系数之和为64,则展开式中的常数项为( )
| 1 |
| x |
| A、10 | B、20 | C、30 | D、35 |
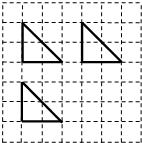 如图,网格纸上的正方形小格的边长为l,图中的粗线画出了某几何体的三视图,则该几何体的表面积是( )
如图,网格纸上的正方形小格的边长为l,图中的粗线画出了某几何体的三视图,则该几何体的表面积是( )A、4+2
| ||
B、4+4
| ||
C、6+2
| ||
D、6+3
|
已知命题P:?x>0,x3>0,那么?P是( )
| A、?x≤0,x3≤0 |
| B、?x>0,x3≤0 |
| C、?x>0,x3≤0 |
| D、?x<0,x3≤0 |
设i是虚数单位,若复数m+
(m∈R)是纯虚数,则m的值为( )
| 10 |
| 3+i |
| A、-3 | B、-1 | C、1 | D、3 |
设集合M={(x,y)|y=2
},N={(x,y)|y=k(x-b)+1},若对任意的0≤k≤1都有M∩N≠∅,则实数b的取值范围是( )
| 1-x2 |
A、[1-
| ||||
| B、[-1,2] | ||||
C、[-1,1+
| ||||
D、[1-
|