题目内容

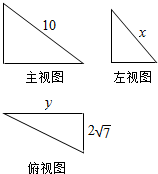
某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy的最大值为（　　）
A、32
B、32
7
C、64
D、64
7
考点：简单空间图形的三视图
专题：不等式的解法及应用,空间位置关系与距离
分析：由已知中的三个视图中的三角形均为直角三角形，设三视图的高为h，则h2+y2=102，且h2+（2
7
）2=x2，进而根据基本不等式可得xy的最大值．
解答： 解：由已知中的三个视图中的三角形均为直角三角形，
设三视图的高为h，
则h2+y2=102，且h2+（2
7
）2=x2，
则x2+y2=128≥2xy，
∴xy≤64，
即xy的最大值为64，
故选：C
点评：本题考查的知识点是简单空间图形的三视图，基本不等式的应用，难度中档．
练习册系列答案
相关题目
已知曲线C1的参数方程为
x=-2+
10
cosθ
y=
10
sinθ
(θ为参数），曲线C2的极坐标方程为ρ=2cosθ+6sinθ，问曲线C1，C2是否相交，若相交请求出公共弦的方程，若不相交，请说明理由．
双曲线
x2
a2
-
y2
b2
=1与曲线
x2
3a2
+
y2
b2
=1（a＞0，b＞0）的交点恰为某正方形的四个顶点，则双曲线的离心率为（　　）
A、3
B、2
C、
3
D、
2
对于正项数列{an}，若
an+1
an
≥q对一切n∈N*恒成立，则an≥a1•qn-1对n∈N*也恒成立是真命题．
（1）若a1=1，an＞0，且
an+1
an
≥3c(c≠
1
3
，c≠1)，求证：数列{an}前n项和Sn≥
1-(3c)n
1-3c
；
（2）若x1=4，xn=
2xn-1+3
(n≥2，n∈N*)，求证：3-(
2
3
)n-1≤xn≤3+(
2
3
)n-1．
在Rt△ABC中，CA=CB=3，M，N是斜边AB上的两个动点，且MN=
2
，则
CM
•
CN
的取值范围为（　　）
A、[3，6]
B、[4，6]
C、[2，
5
2
]
D、[2，4]
设函数f（x）=ex+2x-4，g（x）=lnx+2x2-5，若实数a，b分别是f（x），g（x）的零点，则（　　）
A、g（a）＜0＜f（b）
B、f（b）＜0＜g（a）
C、0＜g（a）＜f（b）
D、f（b）＜g（a）＜0
若(x+
1
x
)n的二项式展开式中二项式系数之和为64，则展开式中的常数项为（　　）
A、10B、20C、30D、35
一个质地均匀的正四面体的四个面上分别标示着数字1、2、3、4，一个质地均匀的正八面体的八个面上分别标示着数字1、2、3、4、5、6、7、8，先后抛掷一次正四面体和正八面体．
（Ⅰ）用数对（x，y）标示正四面体上和八面上被压住的两个数字，请列举出全部基本事件；
（Ⅱ）求正四面体上被压住的数字不小于正八面体上被压住的数字的概率；
（Ⅲ）求两个几何体上被压在底部的两个数字之和不超过6的概率．
函数y=sinωx的图象可以看做是把函数y=sinx的图象上所有点的纵坐标保持不变，横坐标缩短到原来的
1
2
倍而得到，那么ω的值为（　　）
A、4
B、2
C、
1
2
D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网