题目内容
15.已知点A的坐标为(4,2),F是抛物线y2=2x的焦点,点M是抛物线上的动点,当|MF|+|MA|取得最小值时,点M的坐标为(2,2).分析 求出焦点坐标和准线方程,把|MF|+|MA|转化为|MA|+|PM|,利用 当P、A、M三点共线时,|MA|+|PM|取得最小值,把y=2代入抛物线y2=2x 解得x值,即得M的坐标.
解答  解:由题意,F($\frac{1}{2}$,0),准线方程为x=-$\frac{1}{2}$,
解:由题意,F($\frac{1}{2}$,0),准线方程为x=-$\frac{1}{2}$,
设M到准线的距离d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,
故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=4-(-$\frac{1}{2}$)=$\frac{9}{2}$.
把 y=2代入抛物线y2=2x 得 x=2,故点M的坐标是(2,2),
故答案为:(2,2)
点评 本题考查抛物线的定义和性质应用,解答的关键利用是抛物线定义,体现了转化的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知函数f(x)=|x|,则下列结论正确的是( )
| A. | 奇函数,在(-∞,0)上是减函数 | B. | 奇函数,在(-∞,0)上是增函数 | ||
| C. | 偶函数,在(-∞,0)上是减函数 | D. | 偶函数,在(-∞,0)上是增函数 |
20.已知a∈R,若方程a2x2+(a+2)y2+4x+8y+5a=0表示圆,则此圆心坐标( )
| A. | (-2,-4) | B. | $(-\frac{1}{2},-1)$ | C. | (-2,-4)或$(-\frac{1}{2},-1)$ | D. | 不确定 |
7.已知A={x|x+1>0},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | A={0,1,2} | B. | {-2} | C. | {-1,0,1} | D. | {-2,-1} |
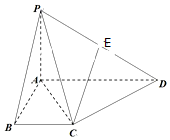 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E为PD的中点.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,∠BAD=90°,AD∥BC,PA=AB=BC=1,AD=2,E为PD的中点. 如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.
如图,在直四棱柱ABCD-A1B1C1D1中(侧棱垂直于底面的四棱柱为直四棱柱),底面四边形ABCD是直角梯形,其中AB⊥AD,AB=BC=1,且AD=$\sqrt{2}$AA1=2.