题目内容
下列关系式正确的是（ ）
A、
| ||
| B、{a，b}={b，a} | ||
| C、{2}={x|x2=2x} | ||
| D、∅∈{2014} |
考点：集合的相等
专题：集合
分析：分别利用集合的定义以及集合元素之间的关系进行判断．
解答：
解：A．
是无理数，Q表示有理数，所以A错误．
B．两个集合的元素都是a，b，根据元素的无序性和集合相等的定义可知，B正确．
C．{x|x2=2x}={0，2}≠{2}，C错误；
D．集合和集合之间的关系不能用“属于”号，所以D错误．
故选B．
| 2 |
B．两个集合的元素都是a，b，根据元素的无序性和集合相等的定义可知，B正确．
C．{x|x2=2x}={0，2}≠{2}，C错误；
D．集合和集合之间的关系不能用“属于”号，所以D错误．
故选B．
点评：本题考查集合的定义以及集合之间的关系，属于基础题．
练习册系列答案
相关题目
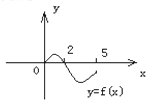若一个函数y=f（x）的图象关于y轴对称，则称这个函数为偶函数，设偶函数y=f（x）的定义域为[-5，5]，若当x∈[0，5]时，函数y=f（x）的图象如下图，则f（x）＜0解集是（ ）| A、（-2，0）∪（2，5] |
| B、（-5，-2）∪（2，5） |
| C、[-2，0]∪（2，5] |
| D、[-5，-2）∪（2，5] |
下列函数中是奇函数的是（ ）
| A、y=x+x2 | ||
| B、y=|x|-2 | ||
C、y=
| ||
| D、y=-x2+1 |
设A={y|y=-1+x-2x2}，若m∈A，则必有（ ）
| A、m∈{正有理数} |
| B、m∈{负有理数} |
| C、m∈{正实数} |
| D、m∈{负实数} |
设各项均不为0的数列{an}满足an+1=
an（n≥1），Sn是其前n项和，若a2a4=2a5，则S4=（ ）
| 2 |
A、4
| ||
B、8
| ||
C、3+3
| ||
D、6+6
|