题目内容
把函数f（x）的图象向右平移一个单位长度，所得图象恰与函数y=ex的图象关于直线y=x对称，则f（x）=（ ）
| A、ln（x-1） |
| B、lnx-1 |
| C、ln（x+1） |
| D、lnx+1 |
考点：反函数
专题：函数的性质及应用
分析：与函数y=ex的图象关于直线y=x对称的函数为y=lnx，只需把y=lnx向左平移一个单位长度即可．
解答：
解：由题意可知与函数y=ex的图象关于直线y=x对称的函数为y=lnx，
只需把y=lnx向左平移一个单位长度得到y=ln（x+1），
∴f（x）=ln（x+1），
故选：C
只需把y=lnx向左平移一个单位长度得到y=ln（x+1），
∴f（x）=ln（x+1），
故选：C
点评：本题考查反函数，属基础题．
练习册系列答案
相关题目
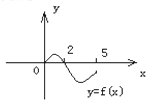若一个函数y=f（x）的图象关于y轴对称，则称这个函数为偶函数，设偶函数y=f（x）的定义域为[-5，5]，若当x∈[0，5]时，函数y=f（x）的图象如下图，则f（x）＜0解集是（ ）| A、（-2，0）∪（2，5] |
| B、（-5，-2）∪（2，5） |
| C、[-2，0]∪（2，5] |
| D、[-5，-2）∪（2，5] |
已知集合A{1，2}，B={1，2}，则可以确定不同映射f：A→B的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
下列函数中是奇函数的是（ ）
| A、y=x+x2 | ||
| B、y=|x|-2 | ||
C、y=
| ||
| D、y=-x2+1 |
设A={y|y=-1+x-2x2}，若m∈A，则必有（ ）
| A、m∈{正有理数} |
| B、m∈{负有理数} |
| C、m∈{正实数} |
| D、m∈{负实数} |