题目内容
下列说法正确的是（ ）
| A、某事件发生的频率是客观存在的，与试验次数无关 |
| B、某事件发生的概率为0，则该事件是不可能事件 |
| C、某事件发生的概率是随机的，在实验前不能确定 |
| D、每个实验结果出现的频率之和一定等于1 |
考点：命题的真假判断与应用
专题：概率与统计
分析：本题考查知识点是随机事件频率与概率的概念，理解概念，抓住本质求解：概率是定值，客观存在，频率是实验数据，频率是概率的估计值．
解答：
解：A、频率是实验数据，随实验次数而变化，A错误；
B、不可能事件的概率为0，但零概率事件不一定是不可能事件例如在几何概率模型中的边界，向圆里扔针，扔到边界的概率的概率近似认为是0，0，而其显然不是不可能事件是不可能事件．错误B；
C、事件发生的概率是客观存在的，是确定的数值，C错误；
D、每个实验结果中频数之和一定等于总实验次数，所以频率之和也一定等于1，D正确．
故选：D．
B、不可能事件的概率为0，但零概率事件不一定是不可能事件例如在几何概率模型中的边界，向圆里扔针，扔到边界的概率的概率近似认为是0，0，而其显然不是不可能事件是不可能事件．错误B；
C、事件发生的概率是客观存在的，是确定的数值，C错误；
D、每个实验结果中频数之和一定等于总实验次数，所以频率之和也一定等于1，D正确．
故选：D．
点评：易错点在B选项中，要区分开零概率事件和不可能事件，不可能事件的概率为0，而概率为0事件也可能发生．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
函数y=x2+2x-4的定义域是（-2，5]，则其值域是（ ）
| A、（4，31] |
| B、[-5，-4] |
| C、（-5，31] |
| D、[-5，31] |
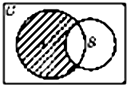已知全集U=R，集合A={y|y=ln（x2+1），x∈R}，集合A={x||x-2|≤1}，则如图所示的阴影部分表示的集合为（ ）| A、{x|0≤x＜1或x＞3} |
| B、{x|0≤x＜1} |
| C、{x|x＞3} |
| D、{x|1≤x≤3} |
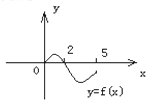若一个函数y=f（x）的图象关于y轴对称，则称这个函数为偶函数，设偶函数y=f（x）的定义域为[-5，5]，若当x∈[0，5]时，函数y=f（x）的图象如下图，则f（x）＜0解集是（ ）| A、（-2，0）∪（2，5] |
| B、（-5，-2）∪（2，5） |
| C、[-2，0]∪（2，5] |
| D、[-5，-2）∪（2，5] |
已知集合A{1，2}，B={1，2}，则可以确定不同映射f：A→B的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
已知集合A={x∈Z|x2-1≤0}，B={x|x2-x-2=0}，则A∩B=（ ）
| A、∅ | B、{-1} |
| C、{0} | D、{2} |