题目内容
15．某食品厂只做了3种与“福”字有关的精美卡片，分别是“富强福”、“和谐福”、“友善福”、每袋食品随机装入一张卡片，若只有集齐3种卡片才可获奖，则购买该食品4袋，获奖的概率为（ ）| A． | $\frac{3}{16}$ | B． | $\frac{4}{9}$ | C． | $\frac{3}{8}$ | D． | $\frac{8}{9}$ |
分析 购买该食品4袋，购买卡片编号的所有可能结果为：n=34，获奖时至多有2张卡片相同，且“富强福”、“和谐福”、“友善福”三种卡片齐全，由此能求出购买该食品4袋，获奖的概率．
解答 解：购买该食品4袋，购买卡片编号的所有可能结果为：n=34，
获奖时至多有2张卡片相同，且“富强福”、“和谐福”、“友善福”三种卡片齐全，
相同的2张为${C}_{3}^{1}$，在4个位置中选2个位置，有${C}_{4}^{2}$种选法，
其余2个卡片有${A}_{2}^{2}$种选法，
∴获奖包含的基本事件个数m=${C}_{3}^{1}{C}_{4}^{2}{A}_{2}^{2}$=36，
∴购买该食品4袋，获奖的概率为p=$\frac{36}{{3}^{4}}$=$\frac{4}{9}$．
故选：B．
点评 本题考查丰典概型及应用，考查概率的计算，考查计数原理，考查排列组合，解答本题的关系是正确理解获奖的情形，解题时要认真审题，注意排列组合公式的合理运用，是中档题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
5．已知函数f（x）=log2x，x∈[1，8]，则不等式1≤f（x）≤2成立的概率是（ ）
| A． | $\frac{1}{7}$ | B． | $\frac{2}{7}$ | C． | $\frac{3}{7}$ | D． | $\frac{4}{7}$ |
6．设F1，F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，双曲线上存在一点P使得∠F1PF2=60°，|OP|=3b（O为坐标原点），则该双曲线的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{7}{6}$ | D． | $\frac{\sqrt{42}}{6}$ |
如图所示的空间几何体中，底面四边形ABCD为正方形，AF⊥AB，AF∥BE，平面ABEF⊥平面ABCD，DF=$\sqrt{5}$，CE=2$\sqrt{2}$，BC=2．
10．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期是π，将函数f（x）的图象向左平移$\frac{π}{6}$个单位长度后得到函数图象过点P（0，1），则函数f（x）=sin（ωx+φ）（ ）
| A． | 有一个对称中心（$\frac{π}{12}$，0） | B． | 有一条对称轴x=$\frac{π}{6}$ | ||
| C． | 在区间[-$\frac{π}{12}$，$\frac{5π}{12}$]上单调递减 | D． | 在区间[-$\frac{π}{12}$，$\frac{5π}{12}$]上单调递增 |
20．某学校需从3名男生和2名女生中选出4人，分派到甲、乙、丙三地参加义工活动，其中甲地需要选派2人且至少有1名女生，乙地和丙地各需要选派1人，则不同的选派方法的种数是（ ）
| A． | 18 | B． | 24 | C． | 36 | D． | 42 |
4．函数f（x）=sin（πx+θ）（|θ|＜$\frac{π}{2}$）的部分图象如图，且f（0）=-$\frac{1}{2}$，则图中m的值为（ ）
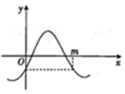
| A． | 1 | B． | $\frac{4}{3}$ | C． | 2 | D． | $\frac{4}{3}$或2 |