题目内容
10.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期是π,将函数f(x)的图象向左平移$\frac{π}{6}$个单位长度后得到函数图象过点P(0,1),则函数f(x)=sin(ωx+φ)( )| A. | 有一个对称中心($\frac{π}{12}$,0) | B. | 有一条对称轴x=$\frac{π}{6}$ | ||
| C. | 在区间[-$\frac{π}{12}$,$\frac{5π}{12}$]上单调递减 | D. | 在区间[-$\frac{π}{12}$,$\frac{5π}{12}$]上单调递增 |
分析 根据最小正周期是π,可得ω,通过变换规律后,图象过点P(0,1),求解φ,可得函数f(x)的解析式,即可判断各选项.
解答 解:由题意,函数f(x)的最小正周期是π,即$\frac{2π}{ω}=π$,∴ω=2.
∴f(x)=sin(2x+φ),
f(x)的图象向左平移$\frac{π}{6}$个单位,可得:sin(2x+$\frac{π}{3}$+φ),此时图象过P(0,1),
可得:$\frac{π}{3}$+φ=$\frac{π}{2}$+2kπ,k∈Z,
∵0<φ<π,
∴φ=$\frac{π}{6}$.
∴f(x)=sin(2x+$\frac{π}{6}$),
令$-\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$是单调递增,
可得:$-\frac{π}{3}+kπ$$≤x≤\frac{π}{6}+kπ$,k∈Z,
∴C选项不对,
令$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$是单调递增,
可得:$\frac{π}{6}+kπ$≤x≤$\frac{2π}{3}$+kπ,k∈Z,
∴D选项不对,
由2x+$\frac{π}{6}$=kπ,
得x=$\frac{1}{2}kπ-\frac{π}{12}$
可得对称中心为($\frac{1}{2}kπ-\frac{π}{12}$,0),考查A不对.
由2x+$\frac{π}{6}$=kπ$+\frac{π}{2}$,
得x=$\frac{1}{2}kπ$$+\frac{π}{6}$,
可得对称轴方程为x=$\frac{1}{2}kπ$$+\frac{π}{6}$,
当k=0时,可得x=$\frac{π}{6}$,
∴B选项对.
故选B.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用已知条件求出f(x)解析式是解决本题的关键.属于中档题.

 阅读快车系列答案
阅读快车系列答案| ξ | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
| A. | $\frac{9}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{9}{10}$ |
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时PM2.5的浓度;(II)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| A. | $\frac{3}{16}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{9}$ |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{4}$=1 |
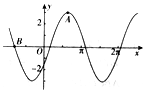 已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).
已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).