题目内容
11.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知atanB=2bsinA.(1)求B;
(2)若b=$\sqrt{3}$,A=$\frac{5π}{12}$,求△ABC的面积.
分析 (1)根据题意,将atanB=2bsinA变形可得asinB=2bsinAcosB,由正弦定理可得sinAsinB=2sinBsinAcosB,分析可得cosB=$\frac{1}{2}$,由B的范围可得答案;
(2)由三角形内角和定理可得C的大小,进而由正弦定理可得c=$\frac{b}{sinB}$×sinC=$\sqrt{2}$,由三角形面积公式S△ABC=$\frac{1}{2}$bcsinA计算可得答案.
解答 解:(1)根据题意,atanB=2bsinA⇒a$\frac{sinB}{cosB}$=2bsinA⇒asinB=2bsinAcosB,
由正弦定理可得sinAsinB=2sinBsinAcosB,
变形可得2cosB=1,即cosB=$\frac{1}{2}$,
又由0<B<π,
故B=$\frac{π}{3}$,
(2)由(1)可得:B=$\frac{π}{3}$,
则C=π-$\frac{π}{3}$-$\frac{5π}{12}$=$\frac{π}{4}$,
由正弦定理$\frac{b}{sinB}$=$\frac{c}{sinC}$,可得c=$\frac{b}{sinB}$×sinC=$\sqrt{2}$,
S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{2}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$=$\frac{3+\sqrt{3}}{4}$.
点评 本题考查了正弦定理余弦定理、三角形面积计算公式、倍角公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.某食品厂只做了3种与“福”字有关的精美卡片,分别是“富强福”、“和谐福”、“友善福”、每袋食品随机装入一张卡片,若只有集齐3种卡片才可获奖,则购买该食品4袋,获奖的概率为( )
| A. | $\frac{3}{16}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{9}$ |
16.已知集合A={x|x≤4},B={x|x2>4},则A∩B=( )
| A. | {x|-2<x<2} | B. | {x|x<-2或x>2} | C. | {x|x<-2或2<x≤4} | D. | {x|x<-2或2<x<4} |
6.椭圆两焦点为F1(-4,0),F2(4,0),P在椭圆上,若$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,△PF1F2的面积为9,则该椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$+$\frac{{y}^{2}}{4}$=1 |
16.已知函数f(x)=sin(ωx+φ)(ω>,|φ|<$\frac{π}{2}$),其图象相邻两个对称中心的距离为$\frac{π}{2}$,且f(x+$\frac{π}{6}$)=f(-x),下列判断正确的是 ( )
| A. | 函数f(x)的最小正周期为2π | |
| B. | 函数f(x)的图象关于点($\frac{7π}{12}$,0)对称 | |
| C. | 函数f(x)在[$\frac{3π}{4}$,π]上单调递增 | |
| D. | 函数f(x)的图象关于直线x=-$\frac{7π}{12}$对称 |
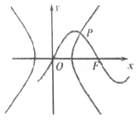 如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )
如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )