题目内容
7.若x,y满足约束条件$\left\{\begin{array}{l}{x<2}\\{x+y-2≥0}\\{x-y+2≥0}\end{array}\right.$,则$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{2}$.分析 作出不等式组对应的平面区域,根据点到直线的距离公式进行求解即可.
解答 解:作出不等式组对应的平面区域如图:
$\sqrt{{x}^{2}+{y}^{2}}$的几何意义是平面区域内的点到原点的距离,
由图象得O到直线x+y-2=0的距离最小,
此时最小值d=$\frac{|0+0-2|}{\sqrt{2}}$=$\sqrt{2}$,
则$\sqrt{{x}^{2}+{y}^{2}}$的最小值是$\sqrt{2}$,
故答案为:$\sqrt{2}$
点评 本题主要考查线性规划的应用,利用点到直线的距离公式结合数形结合是解决本题的关键.

练习册系列答案
相关题目
17.5个车位分别停放了A,B,C,D,E,5辆不同的车,现将所有车开出后再按A,B,C,D,E的次序停入这5个车位,则在A车停入了B车原来的位置的条件下,停放结束后恰有1辆车停在原来位置上的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{40}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
18.2015年12月,华中地区数城市空气污染指数“爆表”,此轮污染为2015年以来最严重的污染过程,为了探究车流量与PM2.5的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:
(1)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;(提示数据:$\sum_{i=1}^7{{x_i}{y_i}=1372}$)
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时PM2.5的浓度;(II)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时PM2.5的浓度;(II)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$.
15.某食品厂只做了3种与“福”字有关的精美卡片,分别是“富强福”、“和谐福”、“友善福”、每袋食品随机装入一张卡片,若只有集齐3种卡片才可获奖,则购买该食品4袋,获奖的概率为( )
| A. | $\frac{3}{16}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{9}$ |
2.已知正方形ABCD的边长为1,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,$\overrightarrow{CD}$=$\overrightarrow{c}$,则|$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$|等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
16.已知集合A={x|x≤4},B={x|x2>4},则A∩B=( )
| A. | {x|-2<x<2} | B. | {x|x<-2或x>2} | C. | {x|x<-2或2<x≤4} | D. | {x|x<-2或2<x<4} |
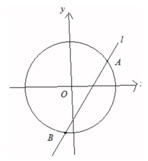 已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.
已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.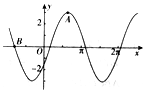 已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).
已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).