题目内容
4.函数f(x)=sin(πx+θ)(|θ|<$\frac{π}{2}$)的部分图象如图,且f(0)=-$\frac{1}{2}$,则图中m的值为( )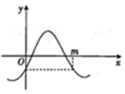
| A. | 1 | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{4}{3}$或2 |
分析 f(0)=-$\frac{1}{2}$,则sinθ=-$\frac{1}{2}$,求出θ,利用正弦函数的对称性,即可得出结论.
解答 解:f(0)=-$\frac{1}{2}$,则sinθ=-$\frac{1}{2}$,
∵|θ|<$\frac{π}{2}$,∴θ=-$\frac{π}{6}$,
∴πx-$\frac{π}{6}$=2kπ+$\frac{π}{2}$,∴x=2k+$\frac{2}{3}$,
∴$\frac{m}{2}$=$\frac{2}{3}$,∴m=$\frac{4}{3}$,
故选B.
点评 本题考查正弦函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
14.现阶段全国多地空气质量指数“爆表”.为探究车流量与PM2.5浓度是否相关,现对北方某中心城市的车流量最大的地区进行检测,现采集到12月某天7个不同时段车流量与PM2.5浓度的数据,如下表:
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)规定当PM2.5浓度平均值在(0,50],空气质量等级为优;当PM2.5浓度平均值在(50,100],空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y=\widehatb\overline x$.
| 车流量x(万辆/小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5浓度y(微克/立方米) | 30 | 36 | 38 | 40 | 42 | 44 | 50 |
(2)规定当PM2.5浓度平均值在(0,50],空气质量等级为优;当PM2.5浓度平均值在(50,100],空气质量等级为良;为使该城市空气质量为优和良,利用该回归方程,预测要将车流量控制在每小时多少万辆内(结果以万辆做单位,保留整数).
附:回归直线方程:$\widehaty=\widehatbx+\widehata$,其中$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{(\overline x)}^2}}}=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\widehata=\overline y=\widehatb\overline x$.
15.某食品厂只做了3种与“福”字有关的精美卡片,分别是“富强福”、“和谐福”、“友善福”、每袋食品随机装入一张卡片,若只有集齐3种卡片才可获奖,则购买该食品4袋,获奖的概率为( )
| A. | $\frac{3}{16}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{8}{9}$ |
9.如图,在△ABC中,N、P分别是AC、BN的中点,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{AP}$=( )
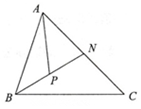

| A. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | B. | -$\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | -$\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ |
16.已知集合A={x|x≤4},B={x|x2>4},则A∩B=( )
| A. | {x|-2<x<2} | B. | {x|x<-2或x>2} | C. | {x|x<-2或2<x≤4} | D. | {x|x<-2或2<x<4} |
 已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.
已知椭圆T:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l经过点P(m,0)与T相交于A、B两点.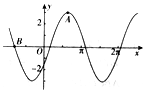 已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).
已知函数f(x)=Msin(ωx+φ)(M>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,其中A(2,3)(点A为图象的一个最高点),B(-$\frac{5}{2}$,0),则函数f(x)=3sin($\frac{π}{3}$x-$\frac{π}{6}$).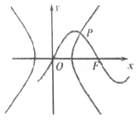 如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )
如图所示,已知函数y=$\sqrt{2}$sin$\frac{π}{4}$x经过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F,函数y=$\sqrt{2}$sin$\frac{π}{4}$x与双曲线在第一象限交点为P,P的横坐标为3,则双曲线的渐近线方程为( )