题目内容
已知集合A={1,2,3,4},B={5,6,7},C={8,9}.现在从这三个集合中取出两个集合,再从这两个集合中各取出一个元素,组成一个含有两个元素的集合,则一共可以组成多少个集合( )
| A、24个 | B、36个 |
| C、26个 | D、27个 |
考点:分步乘法计数原理
专题:计算题
分析:从三个集合中取出两个集合,有3种情况,利用分步计数原理分别计算每种情况下各取出一个元素,组成一个含有两个元素的集合的个数,再相加.
解答:
解:从三个集合中取出两个集合,有
=3种取法,
分别是集合A、B;集合A、C;集合B、C.
当取出集合A、B时,从这两个集合中各取出一个元素,组成一个含有两个元素的集合有
=12个;
当取出集合A、C时,从这两个集合中各取出一个元素,组成一个含有两个元素的集合有
×
=8个;
当取出集合B、C时,从这两个集合中各取出一个元素,组成一个含有两个元素的集合有
×
=6个;
∵集合A、B、C的元素各不相同,∴一共可以组成12+8+6=26个集合.
故选C.
| C | 2 3 |
分别是集合A、B;集合A、C;集合B、C.
当取出集合A、B时,从这两个集合中各取出一个元素,组成一个含有两个元素的集合有
| C | 1 4 |
| ×C | 1 3 |
当取出集合A、C时,从这两个集合中各取出一个元素,组成一个含有两个元素的集合有
| C | 1 4 |
| C | 1 2 |
当取出集合B、C时,从这两个集合中各取出一个元素,组成一个含有两个元素的集合有
| C | 1 3 |
| C | 1 2 |
∵集合A、B、C的元素各不相同,∴一共可以组成12+8+6=26个集合.
故选C.
点评:本题考查了分类分步计数原理,要做到分类不遗漏,分步不重叠.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
执行如图所示的程序框图,则输出的a的值为( )(注:“a=2”,即为“a←2”或为“a:=2”.)
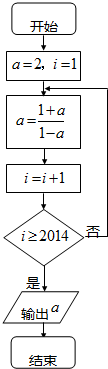

| A、2 | ||
B、
| ||
C、-
| ||
| D、-3 |
复数
的虚部为( )
| -2i |
| 1-i |
| A、i | B、-i | C、1 | D、-1 |
已知△ABC三条边为a,b,c,
=(a,cos
),
=(b,cos
),
=(c,cos
),且三个向量共线,则△ABC的形状是( )
| m |
| A |
| 2 |
| n |
| B |
| 2 |
| p |
| C |
| 2 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是( )


| A、f′(xA)>f′(xB) |
| B、f′(xA)<f′(xB) |
| C、f′(xA)=f′(xB) |
| D、不能确定 |
函数f(x)=8+2x-x2的单调递增区间是( )
| A、[1,+∞) |
| B、(-∞,1] |
| C、[0,1] |
| D、(-∞,+∞ |
| ∫ |
-
|
| A、0 | B、π | C、2 | D、-2 |