题目内容
10．在等比数列{an}中，a2=2，且$\frac{1}{a_1}+\frac{1}{a_3}=\frac{5}{4}$，则a1+a3的值为5．分析 利用等比数列的通项公式即可得出．
解答 解：设等比数列{an}的公比为q，∵a2=2，且$\frac{1}{a_1}+\frac{1}{a_3}=\frac{5}{4}$，
∴$\frac{q}{2}$+$\frac{1}{2q}$=$\frac{5}{4}$，解得q=2或$\frac{1}{2}$．
当q=2时，则a1+a3=$\frac{2}{2}+2×2$=5；
当q=$\frac{1}{2}$时，则a1+a3=$\frac{2}{\frac{1}{2}}$+2×$\frac{1}{2}$=5．
故答案为：5．
点评 本题考查了等比数列的通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
20．若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1与$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率分别为e1，e2，且e1+e2=$\sqrt{3}$，则e1e2=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
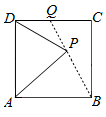如图，在边长为2的正方形ABCD中，点Q边CD上一个动点，$\overrightarrow{CQ}$=λ$\overrightarrow{QD}$，点P为线段BQ（含端点）上一个动点，若λ=1，则$\overrightarrow{PA}$•$\overrightarrow{PD}$的取值范围为[$\frac{4}{5}$，4]．