题目内容
15.已知等差数列{an}的公差为-3,且a3是a1和a4的等比中项,则通项an=-3n+15,数列{an}的前n项和Sn的最大值为30.分析 由题意可得(a1-6)2=a1•(a1-6),解之可得a1,代入通项公式得到an=-3n+15,再判断数列{an}的前n项和Sn的最大值的n的情况,即可求出,
解答 解:由题意可得(a1-6)2=a1•(a1-9),
解得a1=12,
∴an=12+(n-1)×(-3)=-3n+15,
∴an=-3n+15≥0,解得n≤5,
∴S5=5×12+$\frac{5(5-1)×(-3)}{2}$=30,
故答案为:-3n+15,30.
点评 本题考查等差数列的前n项和公式和等比中项的定义,属基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.已知抛物线C1:y2=4x的焦点F恰好是椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点,且两条曲线C1与C2交点的连线过点F,则椭圆C2的长轴长等于( )
| A. | $\sqrt{2}$+1 | B. | 2 | C. | 2$\sqrt{2}$+2 | D. | 4 |
3.已知z(2+i)=1+ai,a∈R,i为虚数单位,若z为纯虚数,则a=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
4.二项式(x-2)5展开式中x的系数为( )
| A. | 5 | B. | 16 | C. | 80 | D. | -80 |
5.函数y=xsinx+cosx的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
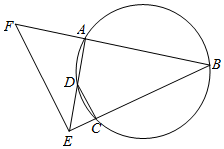 如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,
如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,