题目内容
5．
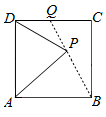如图，在边长为2的正方形ABCD中，点Q边CD上一个动点，$\overrightarrow{CQ}$=λ$\overrightarrow{QD}$，点P为线段BQ（含端点）上一个动点，若λ=1，则$\overrightarrow{PA}$•$\overrightarrow{PD}$的取值范围为[$\frac{4}{5}$，4]．
分析 建立坐标系，由题意利用坐标法求得$\overrightarrow{PA}$•$\overrightarrow{PD}$=5${（k-\frac{4}{5}）}^{2}$+$\frac{4}{5}$，再利用二次函数的性质以及k∈[0，1]，求得它的范围．
解答 
解：以AB所在直线为x轴，以AD 所在直线为y轴，
建立如图所示的坐标系，
可得A（0，0）、B（2，0）、C（2，2）、D（0，2），
当λ=1时，点Q为线段CD的中点，Q（1，2）．
由于点P（x，y）在线段BQ上，故$\overrightarrow{BP}$=k•$\overrightarrow{BQ}$，
即（x-2，y）=k（-1，2），k∈[0，1]，
即 x-2=-k，且y=2k．
∵$\overrightarrow{PA}$•$\overrightarrow{PD}$=（-x，-y）•（-x，2-y）=x2-2y+y2
=（2-k）2-4k+4k2=5k2-8k+4=5${（k-\frac{4}{5}）}^{2}$+$\frac{4}{5}$，
故当k=0时，$\overrightarrow{PA}•\overrightarrow{PD}$取得最大值为4，当 k=$\frac{4}{5}$时，$\overrightarrow{PA}•\overrightarrow{PD}$取得最小值为$\frac{4}{5}$，
故$\overrightarrow{PA}•\overrightarrow{PD}$的范围是[$\frac{4}{5}$，4]，
故答案为：[$\frac{4}{5}$，4]．
点评 本题主要考查两个向量的数量积公式，两个向量坐标形式的运算法则的应用，二次函数的性质，属于中档题．
练习册系列答案
相关题目
如图，已知在等腰梯形ABCD中，AB=4，AB∥CD，∠BAD=45°，E，F，G分别是AB，BC，CD的中点，若$\overrightarrow{EF}$在$\overrightarrow{AG}$方向上的投影为$\frac{7}{10}\sqrt{4+\frac{1}{2}A{D^2}}$，则$\frac{{|\overrightarrow{AB}|}}{{|\overrightarrow{CD}|}}$=（ ）
20．已知平面直角坐标系中两个定点E（3，2），F（-3，2），如果对于常数λ，在函数y=|x+2|+|x-2|-4，（x∈[-4，4]）的图象上有且只有6个不同的点P，使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立，那么λ的取值范围是（ ）
| A． | （-5，-$\frac{9}{5}$） | B． | （-$\frac{9}{5}$，11） | C． | （-$\frac{9}{5}$，-1） | D． | （-5，11） |
17．
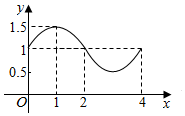函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2013）+f（2014）+f（2015）+f（2016）的值分别为（ ）
函数f（x）=Asin（ωx+φ）+b的图象如图，则f（x）的解析式和S=f（0）+f（1）+f（2）+…+f（2013）+f（2014）+f（2015）+f（2016）的值分别为（ ）| A． | f（x）=$\frac{1}{2}$sin2πx+1，S=2016 | B． | f（x）=$\frac{1}{2}$sin2πx+1，S=2016$\frac{1}{2}$ | ||
| C． | f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2017$\frac{1}{2}$ | D． | f（x）=$\frac{1}{2}$sin$\frac{π}{2}$x+1，S=2017 |