题目内容
20．若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1与$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率分别为e1，e2，且e1+e2=$\sqrt{3}$，则e1e2=（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
分析 由已知得e1=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$，e2=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$，由此利用e1+e2=$\sqrt{3}$，能求出e1e2的值．
解答 解：∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1与$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率分别为e1，e2，
∴e1=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$，e2=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$，
∵e1+e2=$\sqrt{3}$，
∴${{e}_{1}}^{2}+{{e}_{2}}^{2}+2{e}_{1}{e}_{2}$=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}+\frac{{a}^{2}+{b}^{2}}{{a}^{2}}$+2e1e2=2+2e1e2=3，
∴e1e2=$\frac{1}{2}$．
故选：C．
点评 本题考查椭圆方程的求法，是中档题，解题时要认真审题，注意椭圆、双曲线性质的合理运用．
练习册系列答案
相关题目
8．已知椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞0，b＞0）．双曲线C2：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为x$±\sqrt{3}$y=0，则C1与C2的离心率之积为（ ）
| A． | $\frac{{\sqrt{15}}}{4}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{\sqrt{6}}}{5}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
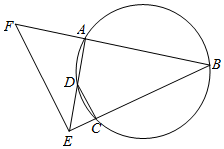如图，A，B，C，D四点共圆，BC，AD的延长线交于点E，点F在BA的延长线上，
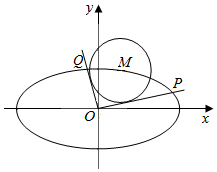如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率e=$\frac{\sqrt{2}}{2}$，M（x0，y0）是椭圆上的任一点，从原点O向圆M：（x-x0）2+（y-y0）2=2作两条切线，分别交椭圆于点P，Q．