已知两点A.设向量$\overrightarrow a=\overrightarrow{AB}$.$\overrightarrow{b}$=(1.m).若$\overrightarrow{a}$⊥$\overrightarrow{b}$.那么实数m=1．题目和参考答案——青夏教育精英家教网——

题目内容

19．已知两点A（0，2）、B（3，-1），设向量$\overrightarrow a=\overrightarrow{AB}$，$\overrightarrow{b}$=（1，m），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，那么实数m=1．

分析由条件利用两个向量坐标形式的运算，两个向量垂直的性质，由$\overrightarrow{a}•\overrightarrow{b}$=0，求得实数m的值．

解答解：∵两点A（0，2）、B（3，-1），设向量$\overrightarrow a=\overrightarrow{AB}$=（3，-3），$\overrightarrow{b}$=（1，m），
若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则$\overrightarrow{a}•\overrightarrow{b}$=3+m（-3）=0，求得实数m=1，
故答案为：1．

点评本题主要考查两个向量坐标形式的运算，两个向量垂直的性质，属于基础题．

练习册系列答案

卓文书业加速度系列答案

新中考复习指导与自主测评系列答案

新中考英语系列答案

中考联通中考冲刺卷系列答案

中考仿真卷系列答案

中考高手系列答案

新支点中考经典系列答案

中考零距离突破系列答案

中考信息猜想卷系列答案

中考专辑精通中考系列答案

相关题目

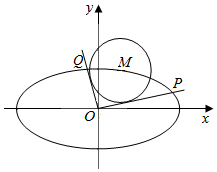如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率e=$\frac{\sqrt{2}}{2}$，M（x₀，y₀）是椭圆上的任一点，从原点O向圆M：（x-x₀）²+（y-y₀）²=2作两条切线，分别交椭圆于点P，Q．
（Ⅰ）若过点（0，-b），（a，0）的直线与原点的距离为$\sqrt{2}$，求椭圆方程；
（Ⅱ）在（Ⅰ）的条件下，若直线OP，OQ的斜率存在，并记为k₁，k₂．试问k₁k₂是否为定值？若是，求出该值；若不是，说明理由．

10．在等比数列{a_n}中，a₂=2，且$\frac{1}{a_1}+\frac{1}{a_3}=\frac{5}{4}$，则a₁+a₃的值为5．

7．已知复数z满足z（1-i）=2i，其中i为虚数单位，则|z|=$\sqrt{2}$．

14．已知双曲线C₁：$\frac{{x}^{2}}{4}$-y²=1，双曲线C₂：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，M是双曲线C₂一条渐近线上的某一点，且OM⊥MF₂，若C₁，C₂的离心率相同，且S${\;}_{△OM{F}_{2}}$=16，则双曲线C₂的实轴长为（　　）

4．二项式（x-2）⁵展开式中x的系数为（　　）

11．已知$0＜α＜\frac{π}{2}$，$sinα=\frac{4}{5}$，$tan（α-β）=-\frac{1}{3}$，则tanβ=3；$\frac{{sin（2β-\frac{π}{2}）•sin（β+π）}}{{\sqrt{2}cos（β+\frac{π}{4}）}}$=$\frac{6}{5}$．

8．求适合下列条件的双曲线的标准方程：
（1）a=2$\sqrt{5}$，过点A（-5，2），焦点在x轴上；
（2）b=1，焦点为（0，±$\sqrt{10}$）：
（3）一个焦点为（-5，0），且离心率为$\frac{5}{4}$．

9．sin410°cos145°+sin680°sin（-35°）=$\frac{\sqrt{2}-\sqrt{6}}{4}$．