题目内容
已知集合A={x|(x-1)(ax2+2x+1)=0,a∈R,x∈R}.
(1)若card(A)=1,求a的取值范围?
(2)若card(A)=2,求a的取值范围?
(3)若card(A)=3,求a的取值范围?
(1)若card(A)=1,求a的取值范围?
(2)若card(A)=2,求a的取值范围?
(3)若card(A)=3,求a的取值范围?
考点:集合的表示法
专题:计算题,集合
分析:(1)方程ax2+2x+1=0无解,或有根1;
(2)card(A)=2,也就意味着方程ax2+2x+1=0只有一个解且不是1;a=0时,方程为一元一次方程,只有一个解,符合条件;a≠0时,方程为一元二次方程,若方程只有一个解,需判别式△=4-4a=0,所以解出a即可,这样a的值就都求出来了.
(3)card(A)=3,即方程ax2+2x+1=0有两个实数根且不是1,即可得出结论.
(2)card(A)=2,也就意味着方程ax2+2x+1=0只有一个解且不是1;a=0时,方程为一元一次方程,只有一个解,符合条件;a≠0时,方程为一元二次方程,若方程只有一个解,需判别式△=4-4a=0,所以解出a即可,这样a的值就都求出来了.
(3)card(A)=3,即方程ax2+2x+1=0有两个实数根且不是1,即可得出结论.
解答:
解:(1)∵集合A={x|(x-1)(ax2+2x+1)=0,a∈R,x∈R},card(A)=1,
∴方程ax2+2x+1=0无解,或有根1,
∴a>1;
(2)card(A)=2,也就意味着方程ax2+2x+1=0只有一个解且不是1;
①当a=0时,方程化为2x+1=0,只有一个解x=-
;
②当a≠0时,若ax2+2x+1=0只有一个解,只需△=4-4a=0,即a=1;
综上所述,可知a的值为a=0或a=1.
(3)card(A)=3,即方程ax2+2x+1=0有两个实数根且不是1.
∴a≠0,且△>0
即a>-1且a≠0.
∴方程ax2+2x+1=0无解,或有根1,
∴a>1;
(2)card(A)=2,也就意味着方程ax2+2x+1=0只有一个解且不是1;
①当a=0时,方程化为2x+1=0,只有一个解x=-
| 1 |
| 2 |
②当a≠0时,若ax2+2x+1=0只有一个解,只需△=4-4a=0,即a=1;
综上所述,可知a的值为a=0或a=1.
(3)card(A)=3,即方程ax2+2x+1=0有两个实数根且不是1.
∴a≠0,且△>0
即a>-1且a≠0.
点评:考查描述法表示集合,一元二次方程的解的求解,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两直线ax-y+2a=0和(2a-1)x+ay+a=0互相垂直,则a=( )
| A、1 | ||||
B、-
| ||||
| C、1或0 | ||||
D、-
|
若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A、-4 | ||
B、-
| ||
C、
| ||
| D、4 |
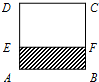 如图E、F是正方形ABCD两边的三等分点,向正方形ABCD内任投一点M,记点M落在阴影区域的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )
如图E、F是正方形ABCD两边的三等分点,向正方形ABCD内任投一点M,记点M落在阴影区域的概率为p,则a=p是函数y=ax2+2x+1有两个零点的( )| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |