题目内容
点P(-2,-1)到直线l:(1+3λ)x+(1+λ)y-2-5λ=0的距离为d,求d的最大值.
考点:点到直线的距离公式
专题:直线与圆
分析:将直线方程变形为x+y-2+(3x+2y-5)λ=0,得直线系恒过点A(1,1),由此得到P到直线l的最远距离为|PA|,此时直线垂直于PA.
解答:
解:∵直线l:(1+3λ)x+(1+λ)y-2-5λ=0,
∴可将直线方程变形为x+y-2+(3x+2y-5)λ=0,
∴
,解得x=1,y=1,
由此可得直线系横过点A(1,1)
则P到直线l的最近距离为A,此时直线过P.
P到直线l的最远距离为|PA|,此时直线垂直于PA.
∴dmax=|PA|=
=
.
∴可将直线方程变形为x+y-2+(3x+2y-5)λ=0,
∴
|
由此可得直线系横过点A(1,1)
则P到直线l的最近距离为A,此时直线过P.
P到直线l的最远距离为|PA|,此时直线垂直于PA.
∴dmax=|PA|=
| (-2-1)2+(-1-1)2 |
| 13 |
点评:本题考查点到直线的距离的最大值的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
已知向量
=(sinx,cosx),
=(1,2)且
⊥
,则tan2x的值为( )
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知集合A={1,2,3},B={2,4},则A∩B=( )
| A、{1} |
| B、{2} |
| C、{1,2} |
| D、{1,2,3,4} |
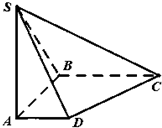 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=2,AD=1.