题目内容
已知锐角α与锐角β的终边上分别有一点(3,4),(
,
).
(Ⅰ)求sinα,cosβ;
(Ⅱ)求tan(α+3π),cos(β-
)的值.
2
| ||
| 5 |
| ||
| 5 |
(Ⅰ)求sinα,cosβ;
(Ⅱ)求tan(α+3π),cos(β-
| π |
| 2 |
考点:任意角的三角函数的定义,运用诱导公式化简求值
专题:三角函数的求值
分析:(Ⅰ)直接利用任意角的三角函数的定义求sinα,cosβ;
(Ⅱ)利用诱导公式化简tan(α+3π),cos(β-
),通过任意角的三角函数的定义求解即可.
(Ⅱ)利用诱导公式化简tan(α+3π),cos(β-
| π |
| 2 |
解答:
解:(Ⅰ)锐角α终边上一点(3,4),所以r=5,sinα=
=
.
锐角β的终边上一点(
,
).R=
=1.
∴cosβ=
;
(Ⅱ)tan(α+3π)=tanα=
=
,
cos(β-
)=sinβ=
.
| y |
| r |
| 4 |
| 5 |
锐角β的终边上一点(
2
| ||
| 5 |
| ||
| 5 |
(
|
∴cosβ=
2
| ||
| 5 |
(Ⅱ)tan(α+3π)=tanα=
| y |
| x |
| 4 |
| 3 |
cos(β-
| π |
| 2 |
| ||
| 5 |
点评:本题考查任意角的三角函数的定义,诱导公式的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线y=
x+5的倾斜角是( )
| ||
| 3 |
| A、30° | B、120° |
| C、60° | D、150° |
复数z在复平面内的对应点为(-1,1),
是z的共轭复数,则
+|z|=( )
. |
| z |
| 2 |
. |
| z |
A、
| ||
B、-
| ||
C、
| ||
D、
|
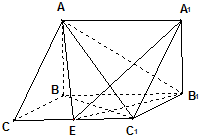 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已BC=1,∠BCC1=