题目内容
过直线x+2y+1=0上点P作圆C：（x+2）2+（y+2）2=1的切线，切点为T，则|PT|的最小值为（ ）
A、
| ||
B、2
| ||
C、
| ||
| D、2 |
考点：圆的切线方程
专题：直线与圆
分析：求出圆心C（-2，-2）到直线x+2y+1=0的距离d，可得|PT|的最小值为
，计算求得结果．
| d2-r2 |
解答：
解：要使|PT|最小，需圆心C（-2，-2）到直线x+2y+1=0上的点P的距离最小，
而CP的最小值即圆心C（-2，-2）到直线x+2y+1=0的距离d=
=
，
故|PT|的最小值为
=
=2，
故选：D．
而CP的最小值即圆心C（-2，-2）到直线x+2y+1=0的距离d=
| |-2-4+1| | ||
|
| 5 |
故|PT|的最小值为
| d2-r2 |
| 5-1 |
故选：D．
点评：本题主要考查直线和圆相切的性质，点到直线的距离公式的应用，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
如果圆x2+y2+Dx+Ey+F=0与x轴相切于原点，则（ ）
| A、E≠0，D=F=0 |
| B、D≠0，E≠0，F=0 |
| C、D≠0，E=F=0 |
| D、F≠0，D=E=0 |
已知△ABC的三个顶点坐标分别为A（2，3，1）、B（4，1，-2）、C（6，3，7），则△ABC的重心坐标为（ ）
A、（6，
| ||
B、（4，
| ||
C、（8，
| ||
D、（2，
|
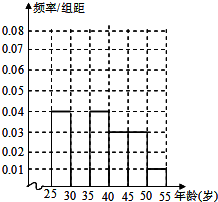某高中社团进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的称为“时尚族”，否则称为“非时尚族”．通过调查分别得到如图所示统计表，如图2所示各年龄段人数频率分布直方图．下列命题中正确的是（ ）
A、“m=
| ||
| B、“直线l垂直平面α内无数条直线”是“直线l垂直于平面α”的充分条件 | ||
| C、已知a，b，c为非零向量，则“a•b=a•c”是“b=c”的充要条件 | ||
| D、p：存在x∈R，x2+2x+2≤0，则￢p：任意x∈R，x2+2x+2＞0． |