题目内容
已知a，b，c是三角形ABC的三条边，且a2+c2-b2=ac，求：
（1）∠B的大小；
（2）若c=3a，求tanA的值．
（1）∠B的大小；
（2）若c=3a，求tanA的值．
考点：余弦定理的应用
专题：综合题,解三角形
分析：（1）直接利用余弦定理即可得到结论；
（2）先将c=3a代入a2+c2-b2=ac，得b=
a，利用余弦定理求出cosA=
=
，再根基同角三角函数之间的关系求出其正弦即可求出结论．
（2）先将c=3a代入a2+c2-b2=ac，得b=
| 7 |
| b2+c2-a2 |
| 2bc |
5
| ||
| 14 |
解答：
解：（1）由余弦定理，得a2+c2-b2=ac=2accosB，
∴cosB=
∵0＜B＜π，
∴B=
；
（2）将c=3a代入a2+c2-b2=ac，得b=
a，
由余弦定理，得cosA=
=
．
∵0＜A＜π，
∴sinA=
=
∴tanA=
．
∴cosB=
| 1 |
| 2 |
∵0＜B＜π，
∴B=
| π |
| 3 |
（2）将c=3a代入a2+c2-b2=ac，得b=
| 7 |
由余弦定理，得cosA=
| b2+c2-a2 |
| 2bc |
5
| ||
| 14 |
∵0＜A＜π，
∴sinA=
| 1-cos2A |
| ||
| 14 |
∴tanA=
| ||
| 5 |
点评：本题考查了解三角形的知识，对余弦定理及其变式进行重点考查，属于中档题目，只要细心分体已知条件式子的特点就不难解答这类问题
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
按如图所示的程序框图，若输出的结果为170，则判断框内应填入的条件为（ ）
| A、i≥5 | B、i≥7 |
| C、i≥9 | D、i≥11 |
关于空间两条直线a、b和平面α，下列命题正确的是（ ）
| A、若a∥b，b?α，则a∥α |
| B、若a∥α，b?α，则a∥b |
| C、若a⊥α，b⊥α，则a∥b |
| D、若a∥α，b∥α，则a∥b |
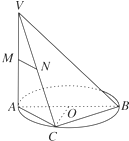如图，AB是⊙O的直径，VA垂直⊙O所在的平面，点C是圆周上不同于A，B的任意一点，M，N分别为VA，VC的中点，则下列结论正确的是（ ）| A、平面VAC⊥平面VBC |
| B、OC⊥平面VAC |
| C、MN与BC所成的角为45° |
| D、MN∥AB |
若椭圆
+
=1（a＞b＞0）的左、右焦点分别为F1、F2，椭圆上一点P，若|PF2|-|PF1|的最大值为2，且当P，F1，F2能构成三角形时，其周长为6，则椭圆方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆的方程为x2+y2-2xlga+2ylg（10a）+2lg2a+2lga=0（a＞0），则圆心所在的直线方程为（ ）
| A、x-y+1=0 |
| B、x+y+1=0 |
| C、x-y-1=0 |
| D、x+y-1=0 |
若函数y=sin（-2x+φ）（|φ|＜
）的图象向左平移
个单位得到y=sin（-2x）的图象，则φ的值为（ ）
| π |
| 2 |
| π |
| 8 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|