题目内容
18.已知集合A={x|lg($\frac{2x-5}{x+2}$)≤0}(1)设U=R,求∁UA;
(2)B={x|x<a},若A⊆B,求a的取值范围;
(3)C={x|m+1≤x≤2m-1}满足C⊆A,求m的取值范围.
分析 求解对数不等式化简A.
(1)直接由补集运算得答案;
(2)直接由集合间的关系求得a的范围;
(3)分C为∅和非空集合讨论,当≠∅时,由集合间的关系列不等式组求解.
解答 解:由lg($\frac{2x-5}{x+2}$)≤0,得0<$\frac{2x-5}{x+2}$≤1,解得:$\frac{5}{2}<x≤7$.
(1)A={x|lg($\frac{2x-5}{x+2}$)≤0}={x|$\frac{5}{2}<x≤7$},又U=R,
∴∁UA={x|x$≤\frac{5}{2}$或x>7};
(2)∵A={x|$\frac{5}{2}<x≤7$},B={x|x<a},
若A⊆B,则a>7;
(3)C={x|m+1≤x≤2m-1},
由C⊆A,若m+1>2m-1,即m<2,C=∅,符合题意;
当m≥2时,要使C⊆A,则$\left\{\begin{array}{l}{m+1>\frac{5}{2}}\\{2m-1≤7}\end{array}\right.$,解得:$\frac{3}{2}<m≤4$.
∴2≤m≤4.
综上,m≤4.
点评 本题考查分式不等式的解法,考查了交、并、补集的混合运算,考查集合间的关系及其应用,关键是对集合端点值间关系的处理,是中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.设f(x)可导,F(x)=f(x)(1+|sinx|),则f(0)=0是F(x)在x=0处可导的( )
| A. | 充分必要条件 | B. | 充分条件但非必要条件 | ||
| C. | 必要条件但非充分条件 | D. | 既非充分条件又非必要条件 |
10.$\sqrt{3}$tan12°+$\sqrt{3}$tan18°+tan12°•tan18°的值是( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 0 | D. | 1 |
7.定义在R上的函数y=f(x)关于y轴对称,且在[0,+∞)上是增加的,则下列关系成立的是( )
| A. | f(3)<f(-4)<f(-π) | B. | f(-π)<f(-4)<f(3) | C. | f(-4)<f(-π)<f(3) | D. | f(3)<f(-π)<f(-4) |
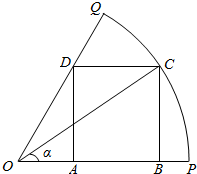 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,