题目内容
17.某几何体的三视图如图所示,则此几何体的体积等于( )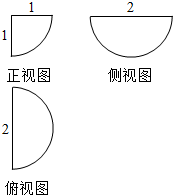
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{8π}{3}$ |
分析 由三视图判断出此几何体是半径为1的球的$\frac{1}{4}$,根据球的体积公式可得答案.
解答 解:由三视图得,此几何体是半径为1的球的$\frac{1}{4}$,
所以此几何体的体积V=$\frac{1}{4}×\frac{4}{3}×π×{1}^{3}$=$\frac{π}{3}$,
故选:B.
点评 本题考查由三视图求几何体的体积,解题关键是判断几何体的形状及几何量所对应的数据,考查空间想象能力.

练习册系列答案
相关题目
7.若f(x)=$\left\{{\begin{array}{l}{sin\frac{πx}{6}(x≤0)}\\{1-2x(x>0)}\end{array}}$,则f(f(3))=( )
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
2.已知α是第四象限角tanα=-$\frac{5}{12}$,则cosα=( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
7.定义在R上的函数y=f(x)关于y轴对称,且在[0,+∞)上是增加的,则下列关系成立的是( )
| A. | f(3)<f(-4)<f(-π) | B. | f(-π)<f(-4)<f(3) | C. | f(-4)<f(-π)<f(3) | D. | f(3)<f(-π)<f(-4) |
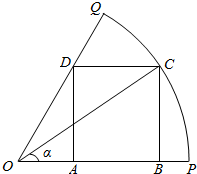 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,