题目内容
14.已知抛物线C1:x2=4y的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$+=1(a>b>0)的一个焦点.C1与C2的公共弦长为2$\sqrt{6}$.(Ⅰ)求C2的方程;
(Ⅱ)过点F的直线l与C1相交于A,B两点,与C2相交于C、D两点,且$\overrightarrow{AC}$,$\overrightarrow{BD}$同向.若|AC|=|BD|,求直线l的斜率.
分析 (1)由抛物线的方程可得C1的焦点坐标,由椭圆的几何性质可得a2-b2=1,结合椭圆、抛物线的对称性分析可得C1与C2的公共点在坐标,将其坐标代入椭圆的方程可得$\frac{9}{4{a}^{2}}$+$\frac{6}{{b}^{2}}$=1,联立两式解可得a2、b2的值,代入椭圆的方程即可得答案;
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),由$\overrightarrow{AC}$,$\overrightarrow{BD}$与同向且|AC|=|BD|分析可得(x1+x2)2-4x1x2=(x3+x4)2-4x3x4①;设直线的斜率为k,则可得直线的方程,联立直线与抛物线的方程,用根与系数的关系表示(x1+x2)和(x1•x2),同理可表示(x3+x4)和(x3•x4),将其值代入①中,解可得k的值.
解答 解:(1)抛物线C1:x2=4y,其开口向上,对称轴为y轴,且其焦点为(0,1),
又由抛物线C1的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的一个焦点,
则有a2-b2=1,
又由C1与C2的公共弦长为2$\sqrt{6}$,而C1与C2的都关于y轴对称,
其公共点在坐标为(±$\sqrt{6}$,$\frac{3}{2}$),
代入椭圆C2:$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1中,可得$\frac{9}{4{a}^{2}}$+$\frac{6}{{b}^{2}}$=1,
解可得a2=9,b2=8,
故椭圆C2的方程为:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{8}$=1;
(2)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
$\overrightarrow{AC}$,$\overrightarrow{BD}$与同向且|AC|=|BD|,则有$\overrightarrow{AC}$=$\overrightarrow{BD}$,
即有x1-x2=x3-x4,
变形可得(x1+x2)2-4x1x2=(x3+x4)2-4x3x4,①
设直线的斜率为k,则直线的方程为y=kx+1,
由$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=4y}\end{array}\right.$,解可得x2-4kx-4=0,有x1+x2=4k,x1•x2=-4,②
由$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{y}^{2}}{9}+\frac{{x}^{2}}{8}=1}\end{array}\right.$,解可得(9+8k2)x2+16kx-64=0,有x3+x4=$\frac{-16k}{9+8{k}^{2}}$,x3x4=$\frac{-64}{9+8{k}^{2}}$③,
将②③代入①中,有(4k)2-4×(-4)=($\frac{-16k}{9+8{k}^{2}}$)2-4×($\frac{-64}{9+8{k}^{2}}$),
解可得k=±$\frac{\sqrt{6}}{4}$;
故直线的斜率k=±$\frac{\sqrt{6}}{4}$.
点评 本题考查椭圆与抛物线的几何性质,涉及直线与抛物线的位置关系,关键是求出椭圆的标准方程.

| A. | $\frac{a-b}{c}$>0 | B. | ac2>bc2 | C. | (a+b)( $\frac{1}{a}$+$\frac{1}{b}$)>4 | D. | a2+b2+2>2a+2b |
| A. | $a>\frac{1}{2}$ | B. | a>$\frac{1}{3}$ | C. | 0<a<$\frac{1}{2}$ | D. | a>0 |
| A. | $\frac{1}{6}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{5}{6}π$ | D. | $\frac{2}{3}π$ |

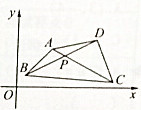 如图所示,已知A(4,5).B(1,2),C(12,1),D(11,6),求AC与BD的交点P的坐标.
如图所示,已知A(4,5).B(1,2),C(12,1),D(11,6),求AC与BD的交点P的坐标.