题目内容
7. 如图所示的三棱柱ABC-A1B1C1中,底面是正三角形,侧棱BB1⊥面ABC,D是棱BC的中点,点M在棱BB1上,且CM⊥AC1.
如图所示的三棱柱ABC-A1B1C1中,底面是正三角形,侧棱BB1⊥面ABC,D是棱BC的中点,点M在棱BB1上,且CM⊥AC1.(1)求证:A1B∥平面AC1D;
(2)求证:CM⊥C1D.
分析 (1)连结A1C,交AC1于N,连结DN,由中位线定理可得DN∥A1B,故而A1B∥平面AC1D;
(2)先证明AD⊥平面BCC1B1,得出AD⊥CM,结合AC1⊥CM得出CM⊥平面ADC1,于是CM⊥C1D.
解答 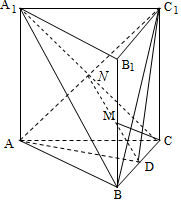 证明:(1)连结A1C,交AC1于N,连结DN,
证明:(1)连结A1C,交AC1于N,连结DN,
∵四边形ACC1A1是平行四边形,
∴N是A1C的中点,又D是BC的中点,
∴DN∥A1B,
又A1B?平面ADC1,DN?平面ADC1,
∴A1B∥平面AC1D.
(2)∵BB1⊥面ABC,AD?平面ABC,
∴BB1⊥AD,
∵△ABC是等边三角形,D是BC的中点,
∴AD⊥BC,又BB1∩BC=B,
∴AD⊥平面BCC1B1,又C1M?平面BCC1B1,
∴AD⊥CM,又CM⊥AC1,AC1∩AD=A,
∴CM⊥平面ADC1,又AC1?平面BCC1B1,
∴CM⊥C1D.
点评 本题考查了线面平行,线面垂直的判定定理,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.曲线f(x)=-$\frac{\sqrt{3}}{3}{x}^{3}$+2在x=1处的切线倾斜角是( )
| A. | $\frac{1}{6}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{5}{6}π$ | D. | $\frac{2}{3}π$ |
17.若函数f(x)=lnx的图象与直线$y=\frac{1}{2}x+a$相切,则a=( )
| A. | 2ln2 | B. | ln2+1 | C. | ln2 | D. | ln2-1 |
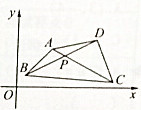 如图所示,已知A(4,5).B(1,2),C(12,1),D(11,6),求AC与BD的交点P的坐标.
如图所示,已知A(4,5).B(1,2),C(12,1),D(11,6),求AC与BD的交点P的坐标.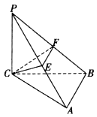 如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.
如图,已知在三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,若PC=BC=8,AB=4,E,F分别是PA,PB的中点,设三棱锥P-CEF的外接球的球心为O,则△AOB的面积为8$\sqrt{5}$.