用数列归纳法证明$\frac{1}{2}+cosα+cos2α+-+cosnα=\frac{{sinα}}{{2sin\frac{α}{2}}}$时.验证n=1时.左边式子为( )A．$\frac{1}{2}$B．cosαC．$\frac{1}{2}+cosα$D．$\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$ 题目和参考答案——青夏教育精英家教网——

题目内容

20．用数列归纳法证明$\frac{1}{2}+cosα+cos2α+…+cosnα=\frac{{sin（n+\frac{1}{2}）α}}{{2sin\frac{α}{2}}}$时，验证n=1时，左边式子为（　　）

A．

$\frac{1}{2}$

B．

cosα

C．

$\frac{1}{2}+cosα$

D．

$\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$

分析把n=1代入左边，得出最后一项即可得出结论．

解答解：当n=1时，左边第一项为$\frac{1}{2}$，最后一项为cosα，
故n=1时，左边式子为$\frac{1}{2}$+cosα，
故选C．

点评本题考查了数学归纳法，属于基础题．

练习册系列答案

名校课堂系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

10．若Z=$\frac{1-2i}{1-i}$，则|Z|=（　　）

$\frac{{\sqrt{2}}}{2}$

$\frac{{\sqrt{3}}}{2}$

$\frac{{\sqrt{5}}}{2}$

$\frac{{\sqrt{10}}}{2}$

11．已知椭圆E的中心在原点，焦点F₁，F₂在y轴上，离心率为$\frac{{2\sqrt{2}}}{3}$，P是椭圆E上的点，以线段PF₁为直径的圆经过F₂，且$9\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=1$．
（Ⅰ）求椭圆E的方程；
（Ⅱ）作直线l与椭圆交于两个不同的点M，N，如果线段MN被直线2x+1=0平分，求直线l的倾斜角的取值范围．

8．△ABC中，已知a=2，b=x，B=60°，如果△ABC 有两组解，则x的取值范围（　　）

$\sqrt{3}＜$x＜2

2＜x＜$\frac{4}{3}$$\sqrt{3}$

2＜x≤$\frac{4}{3}$$\sqrt{3}$

15．下表是一个有i行j列的表格．已知每行每列都成等差数列，

4	7	a_1，3	…	a_1，j
7	12	a_2，3	…	a_2，j
a	a_3，2	a_3，3	…	a_3，j
…	…	…	…	…
a_i，1	a_i，2	a_i，3	…	a_i，j

其中a_i，j表示表格中第i行第j列的数，则a_4，5=49，a_i，j=2ij+i+j．

5．已知变量x，y满足约束条件$\left\{\begin{array}{l}x+2y-3≤0\\ x+3y-3≥0\\ y-1≤0.\end{array}\right.$若目标函数z=ax+y（a＞0）仅在（3，0）点处取得最大值，则a的取值范围是（　　）

$a＞\frac{1}{2}$

a＞$\frac{1}{3}$

0＜a＜$\frac{1}{2}$

12．袋中装有大小相同的4个红球和6个白球，从中取出4个球．
（1）若取出的球必须是两种颜色，则有多少种不同的取法？
（2）若取出的红球个数不少于白球个数，则有多少种不同的取法？

9．曲线f（x）=-$\frac{\sqrt{3}}{3}{x}^{3}$+2在x=1处的切线倾斜角是（　　）

$\frac{1}{6}π$

$\frac{1}{3}π$

$\frac{5}{6}π$

$\frac{2}{3}π$

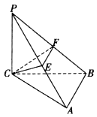如图，已知在三棱锥P-ABC中，PC⊥平面ABC，AB⊥BC，若PC=BC=8，AB=4，E，F分别是PA，PB的中点，设三棱锥P-CEF的外接球的球心为O，则△AOB的面积为8$\sqrt{5}$．