题目内容
19.已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且其图象关于直线$x=\frac{π}{6}$对称.(1)求ω和φ的值;
(2)若$f(\frac{α}{2}-\frac{π}{12})=\frac{3}{5}$,α为锐角,求$cos(α-\frac{π}{3})$的值.
分析 (1)由图象上相邻两个最高点的距离为π,利用正弦函数的图象和性质即可得解?(x)的最小正周期,利用周期公式可求ω,根据对称轴可求φ,
(2)由(1)可得f(x)的解析式,根据两角差的余弦公式即可求出
解答 解:(1)∵$\frac{2π}{ω}=T=π$,
∴ω=2,
∵$2×\frac{π}{6}+φ=\frac{π}{2}+kπ$,
∴$φ=\frac{π}{6}+kπ$,k∈Z,
又0<φ<π,
∴$φ=\frac{π}{6}$.
(2)∵$f(x)=sin(2x+\frac{π}{6})$,
∴$f(\frac{α}{2}-\frac{π}{12})=sinα=\frac{3}{5}$.
∵α为锐角,
∴$cosα=\frac{4}{5}$.
∴$cos(α-\frac{π}{3})=cosαcos\frac{π}{3}+sinαsin\frac{π}{3}=\frac{4}{5}×\frac{1}{2}+\frac{3}{5}×\frac{{\sqrt{3}}}{2}=\frac{{4+3\sqrt{3}}}{10}$.
点评 本题主要考查了正弦函数的图象和性质,三角函数周期公式,两角差的余弦公式,同角三角函数基本关系式,考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了数形结合思想和转化思想,属于中档题.

练习册系列答案
相关题目
10.若Z=$\frac{1-2i}{1-i}$,则|Z|=( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{10}}}{2}$ |
7.若4个人报名参加3项体育比赛,每个人限报一项,则不同的报名方法的种数有( )
| A. | A${\;}_{4}^{3}$ | B. | C${\;}_{4}^{3}$ | C. | 34 | D. | 43 |
14.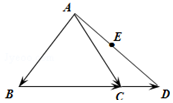 在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )
在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )
 在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )
在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
4.已知a>b>0,c≠0,则下列不等式中不恒成立的是( )
| A. | $\frac{a-b}{c}$>0 | B. | ac2>bc2 | C. | (a+b)( $\frac{1}{a}$+$\frac{1}{b}$)>4 | D. | a2+b2+2>2a+2b |
8.△ABC中,已知a=2,b=x,B=60°,如果△ABC 有两组解,则x的取值范围( )
| A. | x>2 | B. | $\sqrt{3}<$x<2 | C. | 2<x<$\frac{4}{3}$$\sqrt{3}$ | D. | 2<x≤$\frac{4}{3}$$\sqrt{3}$ |
9.曲线f(x)=-$\frac{\sqrt{3}}{3}{x}^{3}$+2在x=1处的切线倾斜角是( )
| A. | $\frac{1}{6}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{5}{6}π$ | D. | $\frac{2}{3}π$ |
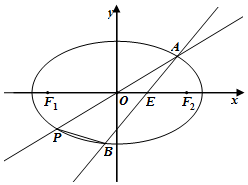 如图,在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{6}}{3}$,a=$\sqrt{6}$,直线l与x轴交于点E,与椭圆C交于A、B两点.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为e=$\frac{\sqrt{6}}{3}$,a=$\sqrt{6}$,直线l与x轴交于点E,与椭圆C交于A、B两点.