题目内容
5．设函数$f（x）=\left\{\begin{array}{l}{x^2}+x，x＜0\\-{x^2}，x≥0\end{array}\right.$，g（x）为定义在R上的奇函数，且当x＜0时，g（x）=x2-2x-5，若f（g（a））≤2，则实数a的取值范围是（ ）| A． | $（{-∞，-1}]∪[{0，2\sqrt{2}-1}]$ | B． | $[{-1，2\sqrt{2}-1}]$ | C． | （-∞，-1]∪（0，3] | D． | [-1，3] |
分析 先将不等式转化为g（a）≥-2，再根据函数的解析式，分类求解．
解答 解：设x＞0，则-x＜0，g（x）=-g（-x）=-x2-2x+5，
由题意，a＜0，a2+a=2，∴a=-2，
∵f（g（a））≤2，$f（x）=\left\{\begin{array}{l}{x^2}+x，x＜0\\-{x^2}，x≥0\end{array}\right.$，∴g（a）≥-2，
∴$\left\{\begin{array}{l}{a＜0}\\{{a}^{2}-2a-5≥-2}\end{array}\right.$或$\left\{\begin{array}{l}{a＞0}\\{-{a}^{2}-2a+5≥-2}\end{array}\right.$或a=0，
∴a≤-1或0≤a≤2$\sqrt{2}$-1，
故选A．
点评 本题考查不等式的解法，考查函数的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
15．定义一种运算a?b=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}\right.$，若f（x）=2x?|x2-4x+3|，当g（x）=f（x）-m有5个零点时，则实数m的取值范围是（ ）
| A． | （0，1） | B． | [0，1] | C． | （1，3） | D． | [1，3] |
13．已知向量$\overrightarrow a=（-2，0），\overrightarrow a-\overrightarrow b=（-3，-1）$，则下列结论正确的是 （ ）
| A． | $\overrightarrow a•\overrightarrow b=2$ | B． | $\overrightarrow a∥\overrightarrow b$ | C． | $|\overrightarrow a|=|\overrightarrow b|$ | D． | $\overrightarrow b⊥（\overrightarrow a+\overrightarrow b）$ |
20．已知复数z满足$\frac{z}{|z|}=\frac{3}{5}+\frac{4}{5}i$，则z的实部与虚部之比为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $-\frac{4}{3}$ | D． | $-\frac{3}{4}$ |
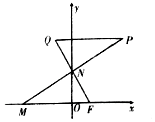已知点F（1，0），动点M，N分别在x轴，y轴上运动，MN⊥NF，Q为平面上一点，$\overrightarrow{NQ}+\overrightarrow{NF}=\overrightarrow 0$，过点Q作QP平行于x轴交MN的延长线于点P．