题目内容
设
,
是两个非零向量,则使
•
=|
||
|成立的一个必要非充分条件是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:平面向量数量积的运算,必要条件、充分条件与充要条件的判断
专题:平面向量及应用
分析:利用向量的数量积求出两个向量的夹角即可推出结果.
解答:
解:∵
,
是两个非零向量,则
•
=|
||
|,
∴
•
=|
||
|cos<
,
>=|
||
|,
∴cos<
,
>=1,
∴<
,
>=0.
∴
∥
.
,
是两个非零向量,则使
•
=|
||
|成立的一个必要非充分条件是
∥
.
故选:D.
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
∴cos<
| a |
| b |
∴<
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选:D.
点评:本题考查向量的数量积以及充要条件的判定,基本知识的应用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知变量x,y满足约束条件
,若x+2y≥-5恒成立,则实数a的取值范围为( )
|
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、[-1,1] |
| D、[-1,1) |
设x,y满足约束条件
,则目标函数z=y-x的最大值是( )
|
| A、5 | B、-1 | C、-5 | D、0 |
下列说法错误的是( )
| A、若命题p:?x∈R,x2-x+1=0,则¬p:?x∈R,x2-x+1≠0 | ||
| B、若命题p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题. | ||
| C、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
D、“sinθ=
|
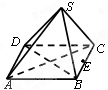 如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持
如图,正四棱锥S-ABCD中,AB=2,E是边BC的中点,动点P在四棱锥的表面上运动,且总保持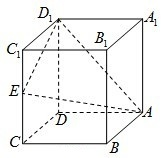 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )
如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )