题目内容
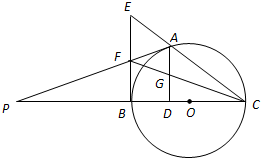如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．（1）求证：BF=EF；
（2）求证：PA是⊙O的切线；
（3）若FG=BF，且的⊙O半径长为3
| 2 |
考点：与圆有关的比例线段
专题：直线与圆
分析：（1）根据切线判定知道EB⊥BC，而AD⊥BC，从而可以确定AD∥BE，那么△BFC∽△DGC，又G是AD的中点，就可得出结论BF=EF．
（2）要证PA是⊙O的切线，就是要证明∠PAO=90°连接AO，AB，根据第1的结论和BE是⊙O的切线和直角三角形的等量代换，就可得出结论．
（3）点F作FH⊥AD于点H，根据前两问的结论，利用三角形的相似性和勾股定理，可以求出BD和FG的长度．
（2）要证PA是⊙O的切线，就是要证明∠PAO=90°连接AO，AB，根据第1的结论和BE是⊙O的切线和直角三角形的等量代换，就可得出结论．
（3）点F作FH⊥AD于点H，根据前两问的结论，利用三角形的相似性和勾股定理，可以求出BD和FG的长度．
解答：
（1）证明：∵BC是圆O的直径，BE是圆O的切线，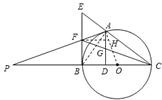
∴EB⊥BC，又∵AD⊥BC，∴AD∥BE，
∴△BFC∽△DGC，△FEC∽△GAC，∴
=
，
∵G是AD的中点，∴DG=AG，∴BF=EF．
（2）证明：连结AO，AB，
∵BC是圆O的直径，∴∠BAC=90°，
在Rt△BAE中，由（1）知F是斜边BE的中点，
∴AF=FB=EF，∴∠FBA=∠FAB，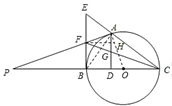
又∵OA=OB，∴∠ABO=∠BAO，
∵BE是圆O的切线，∴∠EBO=90°，
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°，
∴PA是圆O的切线．
（3）解：过点F作FH⊥AD于点H，
∵BD⊥AD，FH⊥AD，∴FH∥BC，
由（2）知∠FBA=∠BAF，∴BF=AF，
由已知得BF=FG，∴AF=FG，∴△AFG是等腰三角形，
∵FH⊥AD，∴AH=GH，∵DG=AG，∴DG=2HG，∴
=
，
∵FH∥BD，BF∥AD，∠FBD=90°，∴四边形BDHF是矩形，BD=FH，
∵FH∥BC，∴△HFG∽△DCG，∴
=
=
=
=
，
∵圆O的半径长为3
，
∴BC=6
．
∴
=
=
=
．
解得BD=2
．∴BD=FH=2
．
∵
=
=
，∴CF=3FG．
在Rt△FBC中，∵CF=3FG，BF=FG，
∴CF2=BF2+BC2，∴（3FG）2=FG2+（6
）2
解得FG=3（负值舍去）
∴FG=3．
∴EB⊥BC，又∵AD⊥BC，∴AD∥BE，
∴△BFC∽△DGC，△FEC∽△GAC，∴
| BF |
| DG |
| EF |
| AG |
∵G是AD的中点，∴DG=AG，∴BF=EF．
（2）证明：连结AO，AB，
∵BC是圆O的直径，∴∠BAC=90°，
在Rt△BAE中，由（1）知F是斜边BE的中点，
∴AF=FB=EF，∴∠FBA=∠FAB，
又∵OA=OB，∴∠ABO=∠BAO，
∵BE是圆O的切线，∴∠EBO=90°，
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°，
∴PA是圆O的切线．
（3）解：过点F作FH⊥AD于点H，
∵BD⊥AD，FH⊥AD，∴FH∥BC，
由（2）知∠FBA=∠BAF，∴BF=AF，
由已知得BF=FG，∴AF=FG，∴△AFG是等腰三角形，
∵FH⊥AD，∴AH=GH，∵DG=AG，∴DG=2HG，∴
| HG |
| DG |
| 1 |
| 2 |
∵FH∥BD，BF∥AD，∠FBD=90°，∴四边形BDHF是矩形，BD=FH，
∵FH∥BC，∴△HFG∽△DCG，∴
| FH |
| CD |
| FG |
| CG |
| HG |
| DG |
| 1 |
| 2 |
| BD |
| CD |
∵圆O的半径长为3
| 2 |
∴BC=6
| 2 |
∴
| BD |
| CD |
| BD |
| BC-BD |
| BD | ||
6
|
| 1 |
| 2 |
解得BD=2
| 2 |
| 2 |
∵
| FG |
| CG |
| HG |
| DG |
| 1 |
| 2 |
在Rt△FBC中，∵CF=3FG，BF=FG，
∴CF2=BF2+BC2，∴（3FG）2=FG2+（6
| 2 |
解得FG=3（负值舍去）
∴FG=3．
点评：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．
练习册系列答案
相关题目