题目内容
17．已知平面上两点A（-1，1），B（5，9），则|AB|=（ ）| A． | 10 | B． | 20 | C． | 30 | D． | 40 |
分析 利用两点间距离公式求解．
解答 解：∵平面上两点A（-1，1），B（5，9），
∴|AB|=$\sqrt{（5+1）^{2}+（9-1）^{2}}$=10．
故选：A．
点评 本题考查两点间距离公式的求法，是基础题，解题时要认真审题，注意两点间距离公式的合理运用．
练习册系列答案
相关题目
8．在△ABC中，a，b，c分别是角A，B，C的对边，a=8，b=4，A=60°，则cosB=（ ）
| A． | $\frac{\sqrt{13}}{4}$ | B． | $\frac{\sqrt{3}}{4}$ | C． | -$\frac{\sqrt{3}}{4}$ | D． | -$\frac{\sqrt{13}}{4}$ |
5．
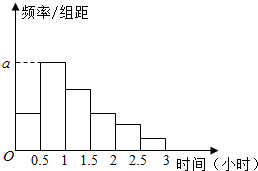随着智能手机等电子产品的普及，“低头族”正成为现代社会的一个流行词．在路上、在餐厅里、在公交车上，随处可见低头玩手机的人，这种“低头族现象”冲击了人们面对面交流的温情，也对人们的健康构成一定的影响．为此，某报社发起一项专题调查，记者随机采访了M名市民，得到这M名市民每人在一天内低头玩手机的时间（单位：小时），根据此数据作出频数的统计表和频率分布直方图如下：
（Ⅰ）求出表中的M，p及图中a的值；
（Ⅱ）试估计这M名市民在一天内低头玩手机的平均时间（同一组的数据用该组的中间值作代表）；
（Ⅲ）在所取样本中，从一天内低头玩手机的时间不少于2小时的市民中任取2人，求两人在一天内低头玩手机的时间都在区间[2，2.5）内的概率．
随着智能手机等电子产品的普及，“低头族”正成为现代社会的一个流行词．在路上、在餐厅里、在公交车上，随处可见低头玩手机的人，这种“低头族现象”冲击了人们面对面交流的温情，也对人们的健康构成一定的影响．为此，某报社发起一项专题调查，记者随机采访了M名市民，得到这M名市民每人在一天内低头玩手机的时间（单位：小时），根据此数据作出频数的统计表和频率分布直方图如下：| 分组 | 频数 | 频率 |
| [0，0.5） | 4 | 0.10 |
| [0.5，1） | m | p |
| [1，1.5） | 10 | n |
| [1.5，2） | 6 | 0.15 |
| [2，2.5） | 4 | 0.10 |
| [2.5，3） | 2 | 0.05 |
| 合计 | M | 1 |
（Ⅱ）试估计这M名市民在一天内低头玩手机的平均时间（同一组的数据用该组的中间值作代表）；
（Ⅲ）在所取样本中，从一天内低头玩手机的时间不少于2小时的市民中任取2人，求两人在一天内低头玩手机的时间都在区间[2，2.5）内的概率．
9．向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，$\overrightarrow{a}$⊥$\overrightarrow{b}$，（$\overrightarrow{a}$-$\overrightarrow{b}$）⊥$\overrightarrow{c}$，$M=\frac{|a|}{|b|}+\frac{|b|}{|c|}+\frac{|c|}{|a|}$，则M=（ ）
| A． | 3 | B． | $3\sqrt{2}$ | C． | $2+\frac{{\sqrt{2}}}{2}$ | D． | $1+\frac{{3\sqrt{2}}}{2}$ |
6．设顶点都在一个球面上的三棱柱的侧棱垂直于底面，所有棱的长都为2，则该球的表面积为（ ）
| A． | 9π | B． | 8π | C． | $\frac{23}{3}π$ | D． | $\frac{28}{3}π$ |
7．已知a，b，c为实数，则a＞b的一个充分不必要条件是（ ）
| A． | a+c＞b+c | B． | ac2＞bc2 | C． | |a|＞|b| | D． | $\frac{a}{b}＞1$ |