题目内容
6．设顶点都在一个球面上的三棱柱的侧棱垂直于底面，所有棱的长都为2，则该球的表面积为（ ）| A． | 9π | B． | 8π | C． | $\frac{23}{3}π$ | D． | $\frac{28}{3}π$ |
分析 由题意可知上下底面中心连线的中点就是球心，求出球的半径，即可求出球的表面积．
解答 
解：根据题意条件可知三棱柱是棱长都为2的正三棱柱，
设上下底面中心连线EF的中点O，则O就是球心，其外接球的半径为OA1，
又设D为A1C1中点，在直角三角形EDA1中，EA1=$\frac{1}{\frac{\sqrt{3}}{2}}$=$\frac{2\sqrt{3}}{3}$
在直角三角形OEA1中，OE=1，由勾股定理得OA1=$\sqrt{1+\frac{4}{3}}$=$\sqrt{\frac{7}{3}}$
∴球的表面积为S=4π•$\frac{7}{3}$=$\frac{28}{3}$π，
故选：D．
点评 本题考查空间几何体中位置关系、球和正棱柱的性质以及相应的运算能力和空间形象能力．
练习册系列答案
相关题目
16．
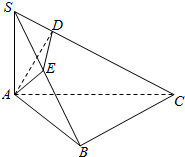如图，在三棱锥S-ABC中，∠ABC=90°，SA⊥平面ABC，点A在SB和SC上的射影分别为E、D．
（1）求证：DE⊥SC；
（2）若SA=AB=BC=1，求直线AD与平面ABC所成角的余弦值．
如图，在三棱锥S-ABC中，∠ABC=90°，SA⊥平面ABC，点A在SB和SC上的射影分别为E、D．（1）求证：DE⊥SC；
（2）若SA=AB=BC=1，求直线AD与平面ABC所成角的余弦值．
17．已知平面上两点A（-1，1），B（5，9），则|AB|=（ ）
| A． | 10 | B． | 20 | C． | 30 | D． | 40 |
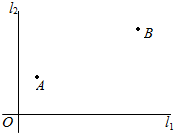如图，在A，B两城周边有两条直线互相垂直的高速公路l1，l2，在点O外交汇，A城到高速公路l1，l2的距离分别是30km，20km，B城到高速公路l1，l2的距离分别是60km，80km，为了方便居民出行，现要在高速公路l1或l2上建造一个高速公路出入口P（不能建造在点O处），经调查，若出入口O建造在高速公路l1上，A，B两城居民的“不满意度”M1=$\frac{1}{2}$（PA+PB），若出入口P建造在高速公路l2上，A，B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$．
18．从1，2，3，4，5，6，7这7个数字中，任取2个数字相加，其和为偶数的概率是（ ）
| A． | $\frac{3}{7}$ | B． | $\frac{4}{7}$ | C． | $\frac{1}{3}$ | D． | $\frac{8}{21}$ |
15．在[-3，4]上随机取一个实数m，能使函数f（x）=x2+mx+1在R上有零点的概率为（ ）
| A． | $\frac{2}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{7}$ |