题目内容
9.向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0,$\overrightarrow{a}$⊥$\overrightarrow{b}$,($\overrightarrow{a}$-$\overrightarrow{b}$)⊥$\overrightarrow{c}$,$M=\frac{|a|}{|b|}+\frac{|b|}{|c|}+\frac{|c|}{|a|}$,则M=( )| A. | 3 | B. | $3\sqrt{2}$ | C. | $2+\frac{{\sqrt{2}}}{2}$ | D. | $1+\frac{{3\sqrt{2}}}{2}$ |
分析 可作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,然后以OA,OB为邻边作平行四边形OACB,而根据条件便可得到AB⊥OC,OA⊥OB,从而得到四边形OACB为正方形,可设该正方形的边长为1,从而可以得出$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,$|\overrightarrow{c}|=\sqrt{2}$,这样便可求出M的值.
解答 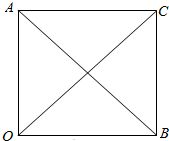 解:根据条件,作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OA}⊥\overrightarrow{OB}$;
解:根据条件,作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OA}⊥\overrightarrow{OB}$;
以OA,OB为邻边作矩形OACB,则$\overrightarrow{OC}=-\overrightarrow{c}$,如图所示,连接OC,AB,则:
$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{a}-\overrightarrow{b}$;
∵$(\overrightarrow{a}-\overrightarrow{b})⊥\overrightarrow{c}$,$\overrightarrow{OC}=-\overrightarrow{c}$;
∴$\overrightarrow{BA}⊥\overrightarrow{OC}$;
即BA⊥OC;
∴矩形OACB为正方形,设边长为1,则:
$|\overrightarrow{a}|=1,|\overrightarrow{b}|=1,|\overrightarrow{c}|=\sqrt{2}$;
∴$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|}+\frac{|\overrightarrow{b}|}{|\overrightarrow{c}|}+\frac{|\overrightarrow{c}|}{|\overrightarrow{a}|}=1+\frac{\sqrt{2}}{2}+\sqrt{2}=1+\frac{3\sqrt{2}}{2}$.
故选D.
点评 考查向量的几何意义,向量加法的平行四边形法则,向量减法的几何意义,清楚正方形的对角线互相垂直,以及数形结合解题的方法.

| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{21}$ |
| A. | -$\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | -$\frac{12}{5}$ | D. | $\frac{12}{5}$ |
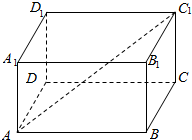 如图,在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,则体对角线AC1与平面ABCD所成角的大小为30°.
如图,在长方体ABCD-A1B1C1D1中,已知A1A=1,AD=1,AB=$\sqrt{2}$,则体对角线AC1与平面ABCD所成角的大小为30°.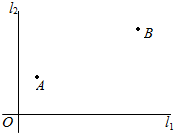 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.