题目内容
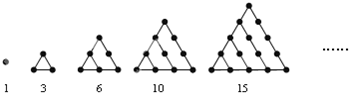
在古希腊，毕达哥拉斯学派把1，3，6，10，15，…这些数叫做三角形数，这是因为这些数目的点可以排成正三角形（如图所示），如图所示，则第七个三角形数是（ ）
| A、30 | B、29 | C、28 | D、27 |
考点：归纳推理
专题：计算题,推理和证明
分析：原来三角形数是从l开始的连续自然数的和．l是第一个三角形数，3是第二个三角形数，6是第三个三角形数，10是第四个三角形数，15是第五个三角形数…那么，第七个三角形数就是：l+2+3+4+5+6+7=28．
解答：
解：原来三角形数是从l开始的连续自然数的和．
l是第一个三角形数，
3是第二个三角形数，
6是第三个三角形数，
10是第四个三角形数，
15是第五个三角形数，
…
那么，第七个三角形数就是：l+2+3+4+5+6+7=28．
故选：C．
l是第一个三角形数，
3是第二个三角形数，
6是第三个三角形数，
10是第四个三角形数，
15是第五个三角形数，
…
那么，第七个三角形数就是：l+2+3+4+5+6+7=28．
故选：C．
点评：本题考查数列在生产实际中的应用，考查运算求解能力，推理论证能力；考查化归与转化思想．综合性强，难度大，易出错，是高考的重点．解题时要认真审题，注意总结规律．
练习册系列答案
相关题目
已知函数y=
的图象与函数y=kx-2的图象恰有两个交点，则实数k的取值范围是（ ）
| |x2-1| |
| x-1 |
| A、（-2，-1）∪（0，4） | ||||
B、（0，
| ||||
C、（
| ||||
| D、（0，1）∪（1，4） |
由1开始的奇数列，按下列方法分组：（1），（3，5），（7，9，11），…，第n组有n个数，则第n组的首项为（ ）
| A、n2-n |
| B、n2-n+1 |
| C、n2+n |
| D、n2+n+1 |
已知cosα=1，a∈[0，2π]，则角α为（ ）
A、
| ||
| B、π | ||
| C、0或2π | ||
| D、2π |
已知函数f（x）=ax2+ax+4（0＜a＜2），若 x1＜x2，x1+x2=1-a，则（ ）
| A、f（x1）＞f（x2） |
| B、f（x1）＜f（x2） |
| C、f（x1）=f（x2） |
| D、f（x1）与f（x2）的大小不能确定 |
已知函数f（x）=
x3-x2-
x，则f（-a2）与f（4）的大小关系为（ ）
| 1 |
| 2 |
| 7 |
| 2 |
| A、f（-a2）≤f（4） |
| B、f（-a2）＜f（4） |
| C、f（-a2）≥f（4） |
| D、f（-a2）与f（4）的大小关系不确定 |
由4，5，6，7，8，9组成没有重复数字且4，8都不与6相邻的六位奇数的个数是（ ）
| A、36 | B、72 | C、96 | D、108 |
下列四个函数中，与y=x表示同一函数的是（ ）
| A、P（-1，3） |
| B、x-2y+3=0 |
| C、a=8 |
| D、y=lg10x |