题目内容
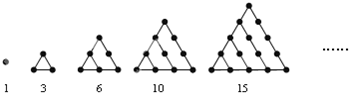
由1开始的奇数列,按下列方法分组:(1),(3,5),(7,9,11),…,第n组有n个数,则第n组的首项为( )
| A、n2-n |
| B、n2-n+1 |
| C、n2+n |
| D、n2+n+1 |
考点:归纳推理
专题:推理和证明
分析:设第n组的首项为an,由题中数列的规律可得a2-a1=2,a3-a2=4,a4-a3=6,…,an-an-1=2(n-1).由此结合题中数据利用等差数列求和公式,即可算出an的通项公式,从而得出第n组的首项.
解答:
解:根据题意,记每一行的第一个数为an,
得:a1=1,a2=3,a3=7,a4=13,…
发现如下规律:
a2-a1=2,a3-a2=4,a4-a3=6,…,an-an-1=2(n-1)
将此n-1个式子相加,得
an-a1=2[1+2+3+…+(n-1)]=2×
=n2-n,
∴an=a1+(n2-n)=n2-n+1,
即第n组的首项为n2-n+1,
故选:B
得:a1=1,a2=3,a3=7,a4=13,…
发现如下规律:
a2-a1=2,a3-a2=4,a4-a3=6,…,an-an-1=2(n-1)
将此n-1个式子相加,得
an-a1=2[1+2+3+…+(n-1)]=2×
| n(n-1) |
| 2 |
∴an=a1+(n2-n)=n2-n+1,
即第n组的首项为n2-n+1,
故选:B
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图,若输入n的值为8,则输出的s的值为( )


| A、29 | B、16 | C、22 | D、11 |
已知2a=5b=10,则(
+
)
=( )
| 2 |
| a |
| 2 |
| b |
| 3 |
| 2 |
A、-2
| ||||
B、2
| ||||
C、-
| ||||
D、
|
已知等比数列{an}中,a1+a2=3,a2+a3=6,则a8=( )
| A、64 | B、128 |
| C、256 | D、512 |
若函数f(x)=
在x=1处可导,则实数a和b的值分别是( )
|
| A、1和0 | B、2和-1 |
| C、1和-2 | D、0和1 |