题目内容
12．函数$f（x）=x{e^x}-\frac{1}{2}{x^2}-x$的零点个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 令f（x）=0，得到ex=-x2+2，作出函数y=ex，和y=-x2+2的图象，利用数形结合即可得到结论．
解答 
解：函数$f（x）=x{e^x}-\frac{1}{2}{x^2}-x$，令f（x）=0，得到x=0或ex=$\frac{1}{2}$x2+1，作出函数y=ex，和y=$\frac{1}{2}$x2+1的图象如图：
由图象可知两个图象的交点公式为1个，
即函数$f（x）=x{e^x}-\frac{1}{2}{x^2}-x$的零点个数为1个，
故选：C．
点评 本题主要考查函数零点公式的判定，利用函数和方程之间的关系转化为两个图象的交点问题是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2．定义函数max$\left\{{f（x），g（x）}\right\}=\left\{{\begin{array}{l}{f（x）（{f（x）≥g（x）}）}\\{g（x）（{f（x）＜g（x）}）}\end{array}}$，则max{sinx，cosx}的最小值为（ ）
| A． | $-\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $-\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
20．
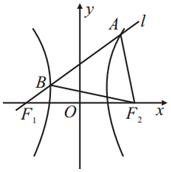如图，F1、F2分别为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左、右焦点，过F1的直线l交C于A、B两点，若C的离心率为$\sqrt{7}$，|AB|=|AF2|，则直线l的斜率为（ ）
如图，F1、F2分别为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左、右焦点，过F1的直线l交C于A、B两点，若C的离心率为$\sqrt{7}$，|AB|=|AF2|，则直线l的斜率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
7．函数f（x）=x3+x2-5x的单调递增区间为（ ）
| A． | $（{-∞，-\frac{5}{3}}）$和（1，+∞） | B． | $（{-∞，-\frac{5}{3}}）∪$（1，+∞） | C． | （-∞，-1）和$（{\frac{5}{3}，+∞}）$ | D． | （-∞，-1）∪$（{\frac{5}{3}，+∞}）$ |
4．用数学归纳法证明1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2n-1}$＜n（n∈N*，n＞1），第一步应验证不等式（ ）
| A． | 1+$\frac{1}{2}$＜2 | B． | 1+$\frac{1}{2}$+$\frac{1}{3}$＜3 | C． | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$＜3 | D． | 1+$\frac{1}{2}$+$\frac{1}{3}$＜2 |
1．
观察图中各正方形图案，每条边上有an个圆点，第an个图案中圆点的个数是an，按此规律推断出所有圆点总和Sn与n的关系式为（ ）
观察图中各正方形图案，每条边上有an个圆点，第an个图案中圆点的个数是an，按此规律推断出所有圆点总和Sn与n的关系式为（ ）| A． | ${S_n}=2{n^2}-2n$ | B． | ${S_n}=2{n^2}$ | C． | ${S_n}=4{n^2}-3n$ | D． | ${S_n}=2{n^2}+2n$ |