题目内容
△ABC的三个角A,B,C所对的边分别是a,b,c,向量
=(2,-1),
=(sinBsinC,
+2cosBcosC),且
⊥
.
(1)求角A的大小.
(2)现给出以下三个条件:①B=45°;②2sinC-(
+1)sinB=0;③a=2.试从中再选择两个条件以确定△ABC,并求出所确定的△ABC的面积.
| m |
| n |
| 3 |
| m |
| n |
(1)求角A的大小.
(2)现给出以下三个条件:①B=45°;②2sinC-(
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,余弦定理
专题:三角函数的求值,平面向量及应用
分析:(1)由
⊥
,可得
•
=0,化为cosA=
,即可得出.
(2)选择①,③.或选择②,③.利用正弦定理与余弦定理、三角形的面积计算公式即可得出.选择①,②不能确定三角形.
| m |
| n |
| m |
| n |
| ||
| 2 |
(2)选择①,③.或选择②,③.利用正弦定理与余弦定理、三角形的面积计算公式即可得出.选择①,②不能确定三角形.
解答:
解:(1)∵
⊥
,
∴
•
=2sinBsinC-2cosBcosC-
=0,
∴cos(B+C)=-
,
∴cosA=
,
又0°<A<180°,
∴A=30°.
(2)选择①,③.
∵A═30°,B=45°,C=105°,a=2且sin105°=sin(45°+60°)=
,
c=
=
+
,
∴S△ABC=
acsinB=
+1.
选②,③.∵A=30°,a=2,
∴2sinC=(
+1)sinB⇒2c=(
+1)b,
由余弦定理:a2=4=b2+(
b)2-2b×
b×
⇒b2=8 b=2
.
c=
b=
+
,
∴S△ABC=
+1.
选①,②不能确定三角形.
| m |
| n |
∴
| m |
| n |
| 3 |
∴cos(B+C)=-
| ||
| 2 |
∴cosA=
| ||
| 2 |
又0°<A<180°,
∴A=30°.
(2)选择①,③.
∵A═30°,B=45°,C=105°,a=2且sin105°=sin(45°+60°)=
| ||||
| 4 |
c=
| asinC |
| sinA |
| 6 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
选②,③.∵A=30°,a=2,
∴2sinC=(
| 3 |
| 3 |
由余弦定理:a2=4=b2+(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
c=
| ||
| 2 |
| 6 |
| 2 |
∴S△ABC=
| 3 |
选①,②不能确定三角形.
点评:本题考查了向量的数量积运算性质、两角和差的正弦余弦公式、正弦定理与余弦定理、诱导公式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知抛物线C1:y=
x2(p>0)的焦点与双曲线C2:
-y2=1的右焦点的连线交C1于第一象限的点M,若C1在点M处的切线平行于C2的一条渐近线,则p=( )
| 1 |
| 2p |
| x2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体8个顶点中任选3个顶点连成三角形,则所得的三角形是等腰直角三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
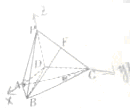 如图,在四棱锥P-ABCD中,底面ABCD是以AC为直径的圆的内接四边形,AC⊥BD,F是PC的中点,∠BAC=60°,PD⊥平面ABC.
如图,在四棱锥P-ABCD中,底面ABCD是以AC为直径的圆的内接四边形,AC⊥BD,F是PC的中点,∠BAC=60°,PD⊥平面ABC.