题目内容
已知tanα，tanβ是方程3x2+5x-7=0的两根，则
= ．
| sin(α+β) |
| cos(α-β) |
考点：两角和与差的正弦函数,两角和与差的余弦函数
专题：三角函数的求值
分析：利用根与系数的关系、两角和差的正弦余弦公式、同角三角函数基本关系式即可得出．
解答：
解：∵tanα，tanβ是方程3x2+5x-7=0的两根，
∴tanα+tanβ=-
，tanα•tanβ=
．
∴
=
=
=
=
．
故答案为：
．
∴tanα+tanβ=-
| 5 |
| 3 |
| -7 |
| 3 |
∴
| sin(α+β) |
| cos(α-β) |
| sinαcosβ+cosαsinβ |
| cosαcosβ+sinαsinβ |
| tanα+atnβ |
| 1+tanαtanβ |
-
| ||
1-
|
| 5 |
| 4 |
故答案为：
| 5 |
| 4 |
点评：本题考查了根与系数的关系、两角和差的正弦余弦公式、同角三角函数基本关系式，属于基础题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
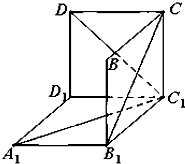如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的．有如下结论：