题目内容
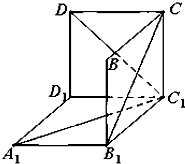 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.有如下结论:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.有如下结论:①∠DC1D1在图中的度数和它表示的角的真实度数都是45°;
②∠A1C1D=∠A1C1D1+∠D1C1D;
③A1C1与BC1所成的角是30°;
④若BC=m,则用图示中这样一个装置盛水,最多能盛
| 1 |
| 6 |
其中正确的结论是
考点:空间中直线与平面之间的位置关系,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:①利用正方体的各个面是正方形的性质即可得出;
②通过正方体计算,即可判断;
③利用对角面的性质、表面对角线组成的△A1C1D是等边三角形即可求出;
④题目中的图形一个装置来盛水,那么盛最多体积的水时应是三棱锥C1-B1CD1的体积.
②通过正方体计算,即可判断;
③利用对角面的性质、表面对角线组成的△A1C1D是等边三角形即可求出;
④题目中的图形一个装置来盛水,那么盛最多体积的水时应是三棱锥C1-B1CD1的体积.
解答:
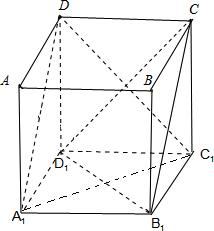 解:补全正方体如图所示:
解:补全正方体如图所示:
①在正视图的等腰直角三角形DC1D1中,∠DC1D1在图中的度数和它表示的角的真实度数都是45°,故①正确;
②由于∠A1C1D=60°,∠A1C1D1+∠D1C1D=45°+45°=90°,
故②错;
③连接A1D.∵A1D=A1C1=DC1,∴△A1C1D是正三角形.
故∠A1C1D=60°.即∠A1C1D的真实度数是60°,故③错;
④用图示中这样一个装置来盛水,那么盛最多体积的水时应是
三棱锥C1-B1CD1的体积.
又V C1-B1D1C=V C-B1C1D1=
×
×1•1•1=
(m3).
∴用图示中这样一个装置来盛水,那么最多可以盛
m3体积的水,故④正确.
故答案为:①④.
 解:补全正方体如图所示:
解:补全正方体如图所示:①在正视图的等腰直角三角形DC1D1中,∠DC1D1在图中的度数和它表示的角的真实度数都是45°,故①正确;
②由于∠A1C1D=60°,∠A1C1D1+∠D1C1D=45°+45°=90°,
故②错;
③连接A1D.∵A1D=A1C1=DC1,∴△A1C1D是正三角形.
故∠A1C1D=60°.即∠A1C1D的真实度数是60°,故③错;
④用图示中这样一个装置来盛水,那么盛最多体积的水时应是
三棱锥C1-B1CD1的体积.
又V C1-B1D1C=V C-B1C1D1=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴用图示中这样一个装置来盛水,那么最多可以盛
| 1 |
| 6 |
故答案为:①④.
点评:本题主要考查了棱柱、棱锥、棱台.熟练掌握正方体对角面、表面对角线的性质及三棱锥的体积计算公式是解题的关键.

练习册系列答案
相关题目