题目内容
已知直线y=a交抛物线x2=4y于A,B两点,若该抛物线上存在点C使得∠ACB为直角,则a的取值范围为 .
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定A(-2
,a),B(2
,a),设C(2m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得
•
=0,即可得到a的取值范围.
| a |
| a |
| AC |
| BC |
解答:
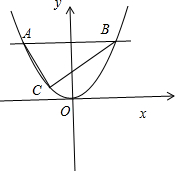 解:如图所示,可知A(-2
解:如图所示,可知A(-2
,a),B(2
,a),
设C(2m,m2),则
=(2m+2
,m2-a),
=(2m-2
,m2-a).
∵该抛物线上存在点C,使得∠ACB为直角,
∴
•
=0,
即4m2-4a+(m2-a)2=0.
∴m2=a-4≥0,解得a≥4.
∴a的取值范围为[4,+∞).
故答案为:[4,+∞).
 解:如图所示,可知A(-2
解:如图所示,可知A(-2| a |
| a |
设C(2m,m2),则
| AC |
| a |
| BC |
| a |
∵该抛物线上存在点C,使得∠ACB为直角,
∴
| AC |
| BC |
即4m2-4a+(m2-a)2=0.
∴m2=a-4≥0,解得a≥4.
∴a的取值范围为[4,+∞).
故答案为:[4,+∞).
点评:本题考查了如何表示抛物线上点的坐标、垂直于数量积得关系等基础知识,考查了推理能力和计算能力.

练习册系列答案
相关题目
直线的参数方程为
(t为参数),则直线的倾斜角为( )
|
| A、40° | B、50° |
| C、140° | D、130° |
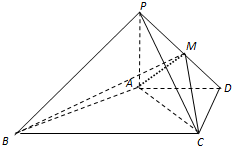 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=