题目内容

16．已知直线l的倾斜角为135°，直线l1经过点A（3，2）和B（a，-1），且直线l1与直线l垂直，直线l2的方程为2x+by+1=0，且直线l2与直线l1平行，则a+b等于（　　）
A．-4B．-2C．0D．2

分析 先求出l的斜率，利用垂直关系可得l1的斜率，由斜率公式求出a 的值，由l1∥l2 得，-$\frac{2}{b}$=1，解得b值，可得结果．

解答 解：∵直线l的斜率为tan135°=-1，l1⊥l，
∴l1的斜率为1，
∴$\frac{2-（-1）}{3-a}=1$，
∴a=0，
∵l1∥l2，
∴l2的斜率为1，
∴$\frac{2}{-b}=1$，
∴b=-2，
∴a+b=-2，
故选：B．

点评 本题考查两直线平行、垂直的性质，斜率公式的应用．

练习册系列答案
相关题目
6．圆C的圆心C（1，2），该圆上一个动点P到直线l：x+y+1=0的距离的最小值为$\sqrt{2}$．
（1）求圆C的标准方程；
（2）过点C作两条互相垂直的直线与直线l交于A，B两个点，求|AB|的最小值．
7．若函数$f（x）=|sinx+\frac{2}{3+sinx}+t|（x，t∈R）$最大值记为g（t），则函数g（t）的最小值为$\frac{3}{4}$．
4．顶点在原点、坐标轴为对称轴的抛物线，过点（-1，2），则它的方程是（　　）
A．y=2x2或y2=-4xB．y2=-4x或x2=2yC．x2=-$\frac{1}{2}$yD．y2=-4x
11．给出下列命题：①直线$x+\sqrt{3}y-1=0$的倾斜角是$\frac{2π}{3}$；②已知过抛物线C：y2=2px（p＞0）的焦点F的直线与抛物线C交于A（x1，y1），B（x2，y2）两点，则有${x_1}{x_2}=\frac{p^2}{4}，{y_1}{y_2}=-{p^2}$；③已知F1、F2为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点，点P为双曲线右支上异于顶点的任意一点，则△PF1F2的内心I始终在一条直线上．
其中所有正确命题的序号为②③．
1．求下列函数的导数．
（1）$y=\frac{e^x}{x}$；           
（2）y=（2x2-1）（3x+1）
8．设等比数列{an}的前n项和为Sn，已知a1=2016，且an+2an+1+an+2=0（n∈N*），则S2016=（　　）
A．0B．2015C．2016D．2017
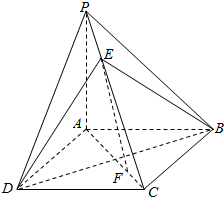5．如图，四棱锥P-ABCD中，底面ABCD是正方形，PA⊥平面ABCD，点E、F在PC、AC上，PE=$\frac{1}{4}$PC．
（I）若EF∥平面PBD，求的$\frac{AF}{AC}$的值；
（II）若PA=AB，三棱锥C-BDE的体积为8，求正方形ABCD的边长．
6．求通项公式：
（1）在数列{an}中，若a1=2，an+1=an+ln（1+$\frac{1}{n}$），则an=2+lnn；
（2）在数列{an}中，若a1=5，an+1=2an+2n+1-1，则an=（n+1）•2n+1；
（3）若an=2an+4n+2，求数列的通项公式；
（4）a1=1，（n+1）a${\;}_{n+1}^{2}$-na${\;}_{n}^{2}$+an+1an=0（n∈N*且an＞0），求数列的通项an；
（5）a1=1，nan=a1+2a2+3a3+…+（n-1）an-1（n≥2，n∈N*），求数列的通项an；
（6）a1=1，an+1=$\frac{{a}_{n}}{-7{a}_{n}-6}$，求数列的通项an；
（7）a1=1，若an+1=a${\;}_{n}^{2}$+2an，求数列的通项an．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网