题目内容
11.给出下列命题:①直线$x+\sqrt{3}y-1=0$的倾斜角是$\frac{2π}{3}$;②已知过抛物线C:y2=2px(p>0)的焦点F的直线与抛物线C交于A(x1,y1),B(x2,y2)两点,则有${x_1}{x_2}=\frac{p^2}{4},{y_1}{y_2}=-{p^2}$;③已知F1、F2为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点,点P为双曲线右支上异于顶点的任意一点,则△PF1F2的内心I始终在一条直线上.其中所有正确命题的序号为②③.
分析 先求出直线的斜率,进而求出直线的倾斜角,可判断①;设出直线方程,联系抛物线方程,根据韦达定理,可判断②;求出I在直线x=a上,可判断③.
解答 解::①直线$x+\sqrt{3}y-1=0$的斜率为:-$\frac{\sqrt{3}}{3}$,故倾斜角是$\frac{5π}{6}$,故错误;
②已知过抛物线C:y2=2px(p>0)的焦点F的直线可设为:x=my+$\frac{p}{2}$,代入抛物线方程得:y2-2pmy-p2=0
菲A(x1,y1),B(x2,y2)两点,则有${y}_{1}{y}_{2}=-{p}^{2}$,则${x}_{1}{x}_{2}=\frac{{p}^{2}}{4}$,故正确;
③已知F1、F2为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点,点P为双曲线右支上异于顶点的任意一点,
设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点M,
则|PA|=|PB|,|F1A|=|F1M|,|F2B|=|F2M|,
又点P在双曲线右支上,
所以|PF1|-|PF2|=2a,故|F1M|-|F2M|=2a,而|F1M|+|F2M|=2c,
设M点坐标为(x,0),
则由|F1M|-|F2M|=2a可得(x+c)-(c-x)=2a
解得x=a,故正确;
故答案为:②③.
点评 本题以命题的真假判断与应用为载体,考查了直线的斜率与倾斜角,直线与圆锥曲线的综合应用,难度中档.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
2.过双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆C2:x2+y2=a2的切线,设切点为M,延长FM交双曲线C1于点N,若点M为线段FN的中点,则双曲线C1的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$+1 | D. | $\frac{\sqrt{5}+1}{2}$ |
19.在正四棱柱ABCD-A1B1C1D1中,AB=2$\sqrt{2}$,AA1=4,E,F分别为棱AB,CD的中点,则三棱锥B1-EFD1的体积为( )
| A. | $\frac{\sqrt{6}}{6}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{16}{3}$ | D. | 16 |
16.已知直线l的倾斜角为135°,直线l1经过点A(3,2)和B(a,-1),且直线l1与直线l垂直,直线l2的方程为2x+by+1=0,且直线l2与直线l1平行,则a+b等于( )
| A. | -4 | B. | -2 | C. | 0 | D. | 2 |
1.已知某圆锥曲线C的极坐标方程是ρ2=$\frac{225}{9+16co{s}^{2}θ}$,则曲线C的离心率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
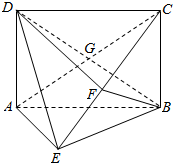 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.