题目内容
已知函数f(x)=
(其中k≥0),若函数y=f[f(x)]+1有4个零点,则实数k的取值范围是 .
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数y=f[f(x)]+1的零点个数,即为方程f[f(x)]=-1的解的个数,结合函数f(x)=
(其中k≥0),求解方程可得答案.
|
解答:
解:当k=0时,函数f(x)=
(其中k≥0)的图象如下图所示:

此时若函数y=f[f(x)]+1=0,则f[f(x)]=-1,
则f(x)=
,只有一解,不合题意,
当0<k<
时,函数f(x)=
(其中k≥0)的图象如下图所示:
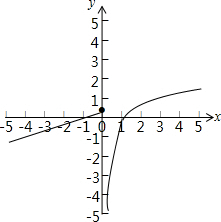
此时若函数y=f[f(x)]+1=0,则f[f(x)]=-1,
则f(x)=
,或kf(x)+k=-1,只有三解,不合题意,
当k≥
时,函数f(x)=
(其中k≥0)的图象如下图所示:

此时若函数y=f[f(x)]+1=0,则f[f(x)]=-1,
则f(x)=
,或kf(x)+k=-1,有四解,满足题意,
故满足条件的实数k的取值范围是[
,+∞),
故答案为:[
,+∞)
|

此时若函数y=f[f(x)]+1=0,则f[f(x)]=-1,
则f(x)=
| 1 |
| e |
当0<k<
| 1 |
| e |
|
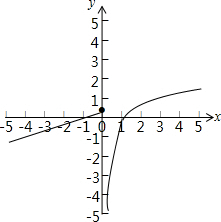
此时若函数y=f[f(x)]+1=0,则f[f(x)]=-1,
则f(x)=
| 1 |
| e |
当k≥
| 1 |
| e |
|

此时若函数y=f[f(x)]+1=0,则f[f(x)]=-1,
则f(x)=
| 1 |
| e |
故满足条件的实数k的取值范围是[
| 1 |
| e |
故答案为:[
| 1 |
| e |
点评:本题考查的知识点是函数零点的判定,其中将函数的零点问题转化为方程根的个数问题,是解答的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
