题目内容
在△ABC中,设
=
,
=
,
=
.若表示
、
、
的有向线段首尾相连能构成三角形,则△ABC的形状是( )
| a |
2
| ||
|
|
| b |
3
| ||
|
|
| c |
4
| ||
|
|
| a |
| b |
| c |
| A、等腰三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、锐角三角形 |
考点:三角形的形状判断,向量在几何中的应用
专题:解三角形,平面向量及应用
分析:利用向量的模的几何意义可知
、
、
的有向线段首尾相连能构成三角形的三边分别为2、3、4,再利用余弦定理即可判断△ABC的形状.
| a |
| b |
| c |
解答:
解:∵|
|=2,|
|=3,|
|=4,
∴以
、
、
的有向线段首尾相连能构成三角形的最大边为4,设最大边所对的角为θ,
则cosθ=
=-
<0,
∴θ为钝角,△ABC为钝角三角形,
故选:C.
| a |
| b |
| c |
∴以
| a |
| b |
| c |
则cosθ=
| 22+32-42 |
| 2×2×3 |
| 1 |
| 4 |
∴θ为钝角,△ABC为钝角三角形,
故选:C.
点评:本题考查△ABC的形状判断,主要考查向量的模的几何意义的应用及余弦定理的应用,考查转化思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知数列{an}的通项公式an=
,Sn为其前n项和,则S6=( )
| 2n-1 |
| 2n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
,则z=
的范围( )
|
| x+1 |
| 2y+1 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、(
|
若O是A、B、P三点所在直线外一点,且满足条件:
=a1
+a4021
,其中{an}为等差数列,则a2011等于( )
| OP |
| OA |
| OB |
A、-
| ||
| B、1 | ||
C、
| ||
| D、-1 |
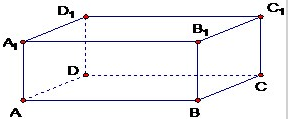 长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).
长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).