题目内容
已知函数f(x)=
sin2x-
-
,若x∈[
,
],求函数f(x)的最值及对应x的值.
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值,三角函数的图像与性质
分析:首先通过恒等变换把函数变形成正弦型函数,利用函数的单调性,进一步求出最值.
解答:
解:知函数f(x)=
sin2x-
-
=sin(2x-
)-1,
若x∈[
,
]
则:
≤2x-
≤
≤sin(2x-
)≤1
所以:-
≤f(x)≤0
当x=
时,函数f(x)的最大值为:0
当x=
时,函数f(x)的最小值为:-
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
若x∈[
| π |
| 4 |
| π |
| 2 |
则:
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
所以:-
| 1 |
| 2 |
当x=
| π |
| 3 |
当x=
| π |
| 2 |
| 1 |
| 2 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的最值,属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“θ≠
”是“cosθ≠
”的( )
| π |
| 3 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )
设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)可能为( )



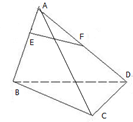 如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.
如图,空间四边形ABCD中,E为AB的三等分点,即AB=3AE,F为AD的中点,求证:直线EF与平面BCD相交.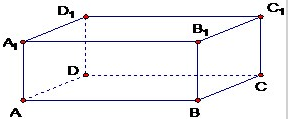 长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).
长方体ABCD-A1B1C1D1中,AB=2,BC=1,AA1=1(利用空间向量求解及证明).