题目内容
已知-
<x<0,sinx+cosx=
.
(1)求sinx-cosx的值;
(2)求
的值.
| π |
| 2 |
| 1 |
| 5 |
(1)求sinx-cosx的值;
(2)求
| 1 |
| cos2x-sin2x |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)将已知等式两边平方,利用完全平方公式展开,再利用同角三角函数间基本关系化简求出sinx-cosx的值即可;
(2)根据(1)的结论与已知等式联立求出sinx与cosx的值,代入原式计算即可得到结果.
(2)根据(1)的结论与已知等式联立求出sinx与cosx的值,代入原式计算即可得到结果.
解答:
解:(1)将sinx+cosx=
,两边平方得:(sinx+cosx)2=1+2sinxcosx=
,
∴2sinxcosx=-
,
则(sinx-cosx)2=1-2sinxcosx=
,
∵-
<x<0,
∴sinx<0,cosx>0,即sinx-cosx<0,
则sinx-cosx=-
;
(2)由已知条件及(1)可知
,
解得:
则
=
=
.
| 1 |
| 5 |
| 1 |
| 25 |
∴2sinxcosx=-
| 24 |
| 25 |
则(sinx-cosx)2=1-2sinxcosx=
| 49 |
| 25 |
∵-
| π |
| 2 |
∴sinx<0,cosx>0,即sinx-cosx<0,
则sinx-cosx=-
| 7 |
| 5 |
(2)由已知条件及(1)可知
|
解得:
|
则
| 1 |
| cos2x-sin2x |
| 1 | ||||
|
| 25 |
| 7 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
设底面为等边三角形的直棱柱的体积为V,则其表面积最小时,底面边长为( )
A、
| |||
B、
| |||
C、
| |||
D、
|
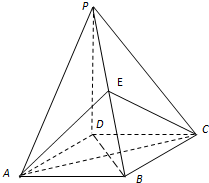 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.