题目内容
已知函数f(x)=x2+2x-3,集合M={(x,y)|f(x)+f(y)≤0,集合N={(x,y)|f(x)-f(y)≥0
(1)求集合M∩N对应区域的面积;
(2)若点P(a,b)∈M∩N,求
的取值范围.
(1)求集合M∩N对应区域的面积;
(2)若点P(a,b)∈M∩N,求
| b |
| a-3 |
考点:函数与方程的综合运用
专题:计算题,作图题,函数的性质及应用,不等式的解法及应用
分析:(1)化简M={(x,y)|(x+1)2+(y+1)2≤8},N={(x,y)|(x-y)(x+y+2)≥0};从而作出平面区域并求面积;
(2)
的几何意义是点P(a,b)与点(3,0)两点连线的直线的斜率,从而求出直线l1与l2的斜率,从而得到
的取值范围.
(2)
| b |
| a-3 |
| b |
| a-3 |
解答:
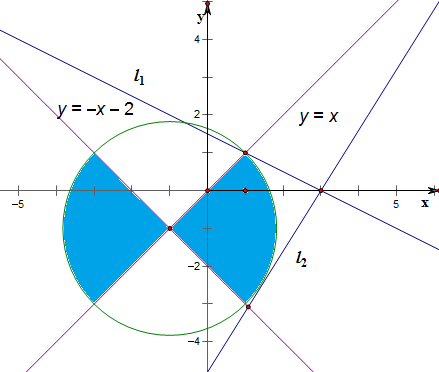 解:(1)化简f(x)+f(y)≤0得,
解:(1)化简f(x)+f(y)≤0得,
(x+1)2+(y+1)2≤8;
故M={(x,y)|(x+1)2+(y+1)2≤8};
f(x)-f(y)≥0得,
(x-y)(x+y+2)≥0;
故N={(x,y)|(x-y)(x+y+2)≥0};
故M∩N的区域如右图,
故其面积S=
•π•8=4π;
(2)
的几何意义是点P(a,b)与点(3,0)两点连线的直线的斜率,
kl1=
=-
,
设l2:y=k(x-3),即kx-y-3k=0,
则
=2
;
解得,k=
(舍去)或k=
;
故kl2=
;
故
的取值范围为[-
,
].
 解:(1)化简f(x)+f(y)≤0得,
解:(1)化简f(x)+f(y)≤0得,(x+1)2+(y+1)2≤8;
故M={(x,y)|(x+1)2+(y+1)2≤8};
f(x)-f(y)≥0得,
(x-y)(x+y+2)≥0;
故N={(x,y)|(x-y)(x+y+2)≥0};
故M∩N的区域如右图,
故其面积S=
| 1 |
| 2 |
(2)
| b |
| a-3 |
kl1=
| 1-0 |
| 1-3 |
| 1 |
| 2 |
设l2:y=k(x-3),即kx-y-3k=0,
则
| |-k+1-3k| | ||
|
| 2 |
解得,k=
2-3
| ||
| 4 |
2+3
| ||
| 4 |
故kl2=
2+3
| ||
| 4 |
故
| b |
| a-3 |
| 1 |
| 2 |
2+3
| ||
| 4 |
点评:本题考查了线性规划的应用,注意集合M与集合N的化简,从而作出平面区域;同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
函数f(x)=lnx+2x-8的零点所在区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
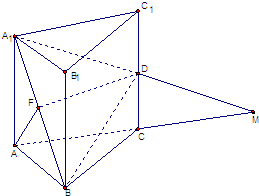 已知:正三棱柱A1B1C1-ABC中,AA1=AB=a,D为CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M.
已知:正三棱柱A1B1C1-ABC中,AA1=AB=a,D为CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M.